今天早上参加了字节跳动的笔试。

4 道题，做出 3 题，遗憾的是不会做的那一题我甚至不知道他考察的算法是什么，以前至少还知道，哦，这是计算几何，我不会，这是动态规划，我写不出来，这次干脆连题目都不知道问的是什么了。
剩下 3 题都比较简单。

第 1 题，找零。

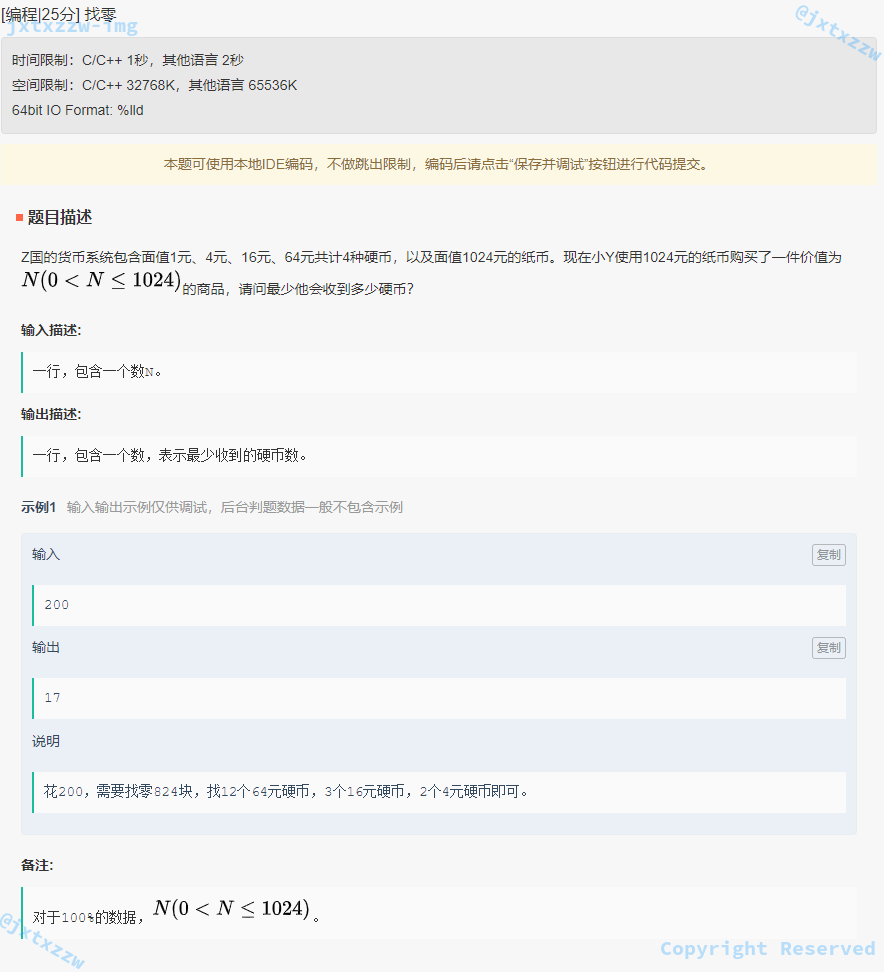
由于货币是 1、4、16、64 成倍数关系，所以贪心成立。

10:04，1 次直接 AC。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int x = 1024 - n;
        int ans = 0;
        int[] a = {1, 4, 16, 64};
        for (int i = a.length - 1; i >= 0;i--) {
            ans += x / a[i];
            x %= a[i];
        }
        System.out.println(ans);
        in.close();
    }
}

第 2 题，万万没想到之聪明的编辑。

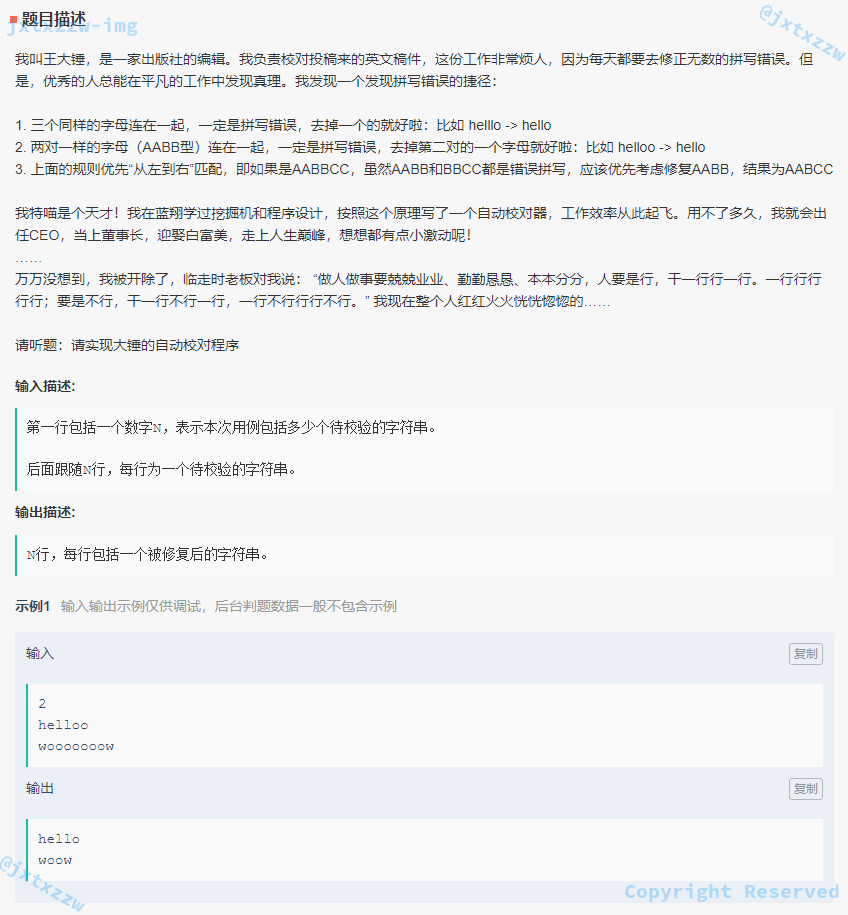
字符串的处理，估计是考查代码能力的，是不是能够足够细心把一步步操作写清楚。

首先从题意可以知道，连续 3 个同样的字母，就消去 1 个，变成 2 个。

并且，显然可以知道，如果有连续 $n$ 个同样的字母，$n \geqslant 3$，那么最终会变成 2 个该字母，例如 wooooooow 中间有 7 个 o，每连续 3 个同样的字母连在一起就去掉一个，那么若干次操作以后会直接变成 oo。

所以，第 1 条规则的化简，就是，如果存在连续 $n$ 个相同的字母，则削减为 2 个。

第 2 条规则，由于说了是从左往右执行的，所以直接模拟。

经过了第 1 条规则的处理以后，剩下的字符串要么是由不同的单字母组成，最多同一个字母连续出现 2 次，从左往右遍历，看是不是存在 AABB 的格式，模拟处理。

难度可能是在于，删除字母以后，字符数组需要将右边的字符左移以填补删除的空位，或者需要构造新的字符串对象，这个操作很容易出错，必须特别小心。

如果用正则表达式来写就非常简单了，这 2 条规则对应的 RegEx 分别是 ("([a-z])\\1{2,}", "$1$1") 和 ("([a-z])\\1{1}([a-z])\\2{1}", "$1$1$2")，很简单，不解释。

10:19，1 次直接 AC。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        for (int i = 0; i < n; i++) {
            String s = in.next();
            s = s.replaceAll("([a-z])\\1{2,}", "$1$1");
            s = s.replaceAll("([a-z])\\1{1}([a-z])\\2{1}", "$1$1$2");
            System.out.println(s);
        }
        in.close();
    }
}

第 3 题，奖品分配。

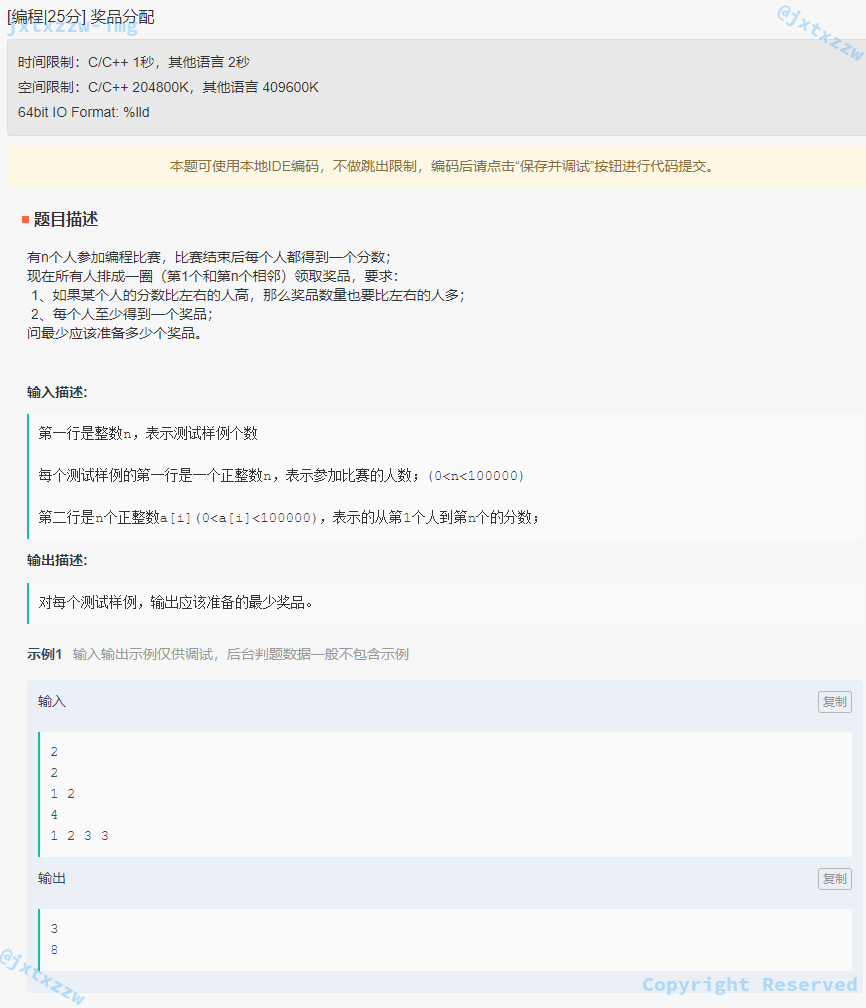
有点难，一下子没有读懂题目意思，所以先做了第 4 题。

第 4 题，剪绳子。

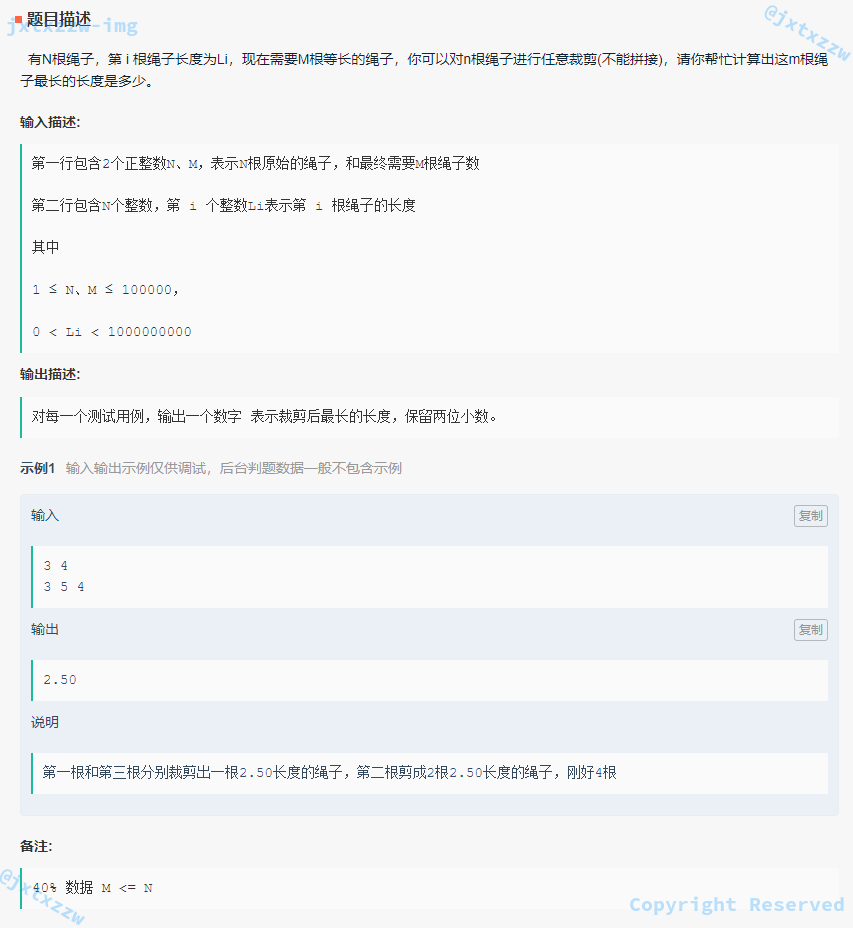
除了样例，还需要注意以下 3 种情况：

• 5 根绳子，分别为 1、2、6、8、9，需要 3 段等长的，显然是 3 段长度为 6 的，似乎是排序以后倒着贪心？
• 5 根绳子，分别为 1、2、3、4、100，需要 2 段等长的，显然是将 100 分为 2 段 50，所以排序不可能了，贪心也不成立。
• 5 根绳子，分别为 1、2、3、50、100，需要 3 段等长的，显然是将 100 分为 2 段 50，加上已经有的那段 50，而不是尝试 100 三等分。

综上，这题既不是贪心（况且贪心已经考过一题了），也不太会是动态规划。

这题的决胜关键在于，花多长时间思考才能意识到这题是二分答案，如果能意识到，那么二分搜索的部分没有任何难度。

左端点是 0，因为显然每一段的长度必须大于 0，右端点是最长的那根绳子，因为不管怎么分，不管分多少段（哪怕是 1 段），都不可能比最长的甚至还长。

二分中点就是期望的裁剪后的长度 $mid$，用这个长度 $mid$ 去算每一根绳子如果切成 $mid$ 长度能够切成多少段，然后加起来。所有段数相加，和目标需要的段数比较。

由于二分中点是浮点数，所以除法结果向下取整计算段数。

• 如果切出来的段数大于目标段数，说明切得太细了，那么左端点变成 $mid$，尝试加大切割长度。
• 如果切出来的段数小于目标段数，说明要减小切割长度，右端点左移。
• 如果切出来的段数等于目标段数，由于题目要求长度尽可能长，所以等效于要加大切割长度，左端点右移。

10:43，1 次直接 AC。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int[] a = new int[n];
        double left = 0;
        int right = 0;
        for (int i = 0; i < n; i++) {
            a[i] = in.nextInt();
            if (a[i] > right) {
                right = a[i];
            }
        }
        double ans = binarySearch(a, left, right, m);
        System.out.printf("%.2f", ans);
        in.close();
    }

    private static double binarySearch(int[] a, double left, double right, int target) {
        while (Math.abs(left - right) > 1E-6) {
            double mid = (left + right) / 2;
            int count = 0;
            for (int x : a) {
                count += (int)(x / mid);
            }
            if (count < target) {
                right = mid;
            } else if (count >= target) {
                left = mid;
            }
        }
        return left;
    }
}

还有 80 分钟，回过头做第 3 题。

首先，理解题目意思花了 30 分钟，到 11:10 左右我才看懂第 2 组样例的那个 8 是怎么回事。

然后开始思考到底这题是考查什么东西。

到了大概 11:20 多，接近 11:30 的时候，弹出一个系统消息，说，第 3 题增加了样例的解释，已更新题目，请刷新页面查看。

我刷新了，然后看到题目下面多了这一句话。

垃圾出题人，害我白花 30 分钟去想那个 “比左右高” 到底是什么意思。

然后还剩 30 分钟，却完全不知道这题考的是什么。

随手糊一个算法上去，通过了 11.11% 的测试数据，剩下的超时。

不管了。

后来问了 zerol，他给出的第 1 个思路是，往图论上面转化。

看成有向图。一个必须比另一个大就连边。想想是不是无环的。如果是那就 DAG 上 DP，可以按拓扑序计算答案（或者记忆化搜索），没出度是 1 否则是 max 后继节点 +1。

后来进一步思考，zerol 给出了简单做法：

所有数字从小到大排，按这个顺序贪心填。其实就是一种拓扑序，注意相同数字相邻的情况。就按一定顺序填，数字从小到大，一批一批填。