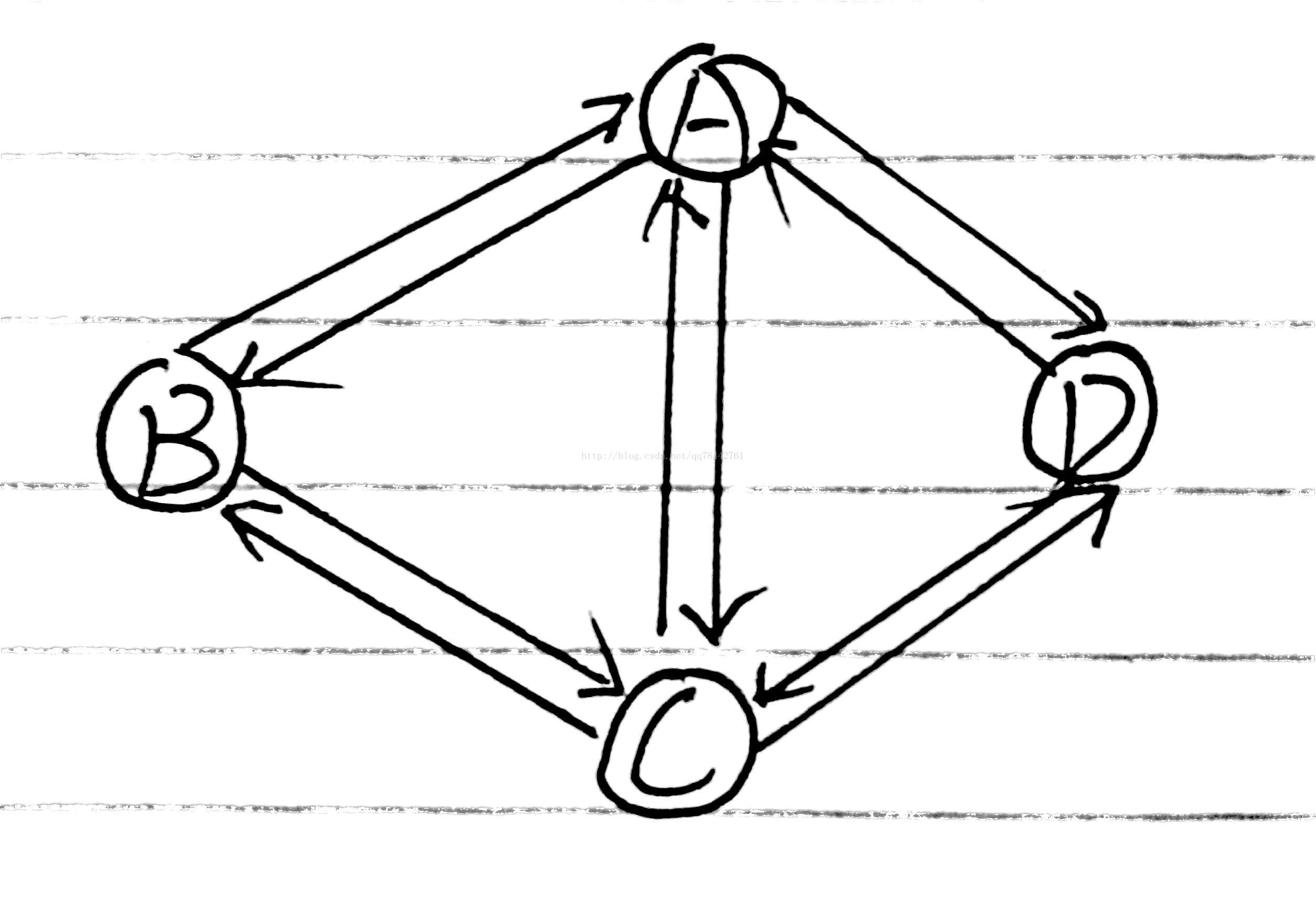
求有向图的强连通分量SCC（Strongly connected component）一般用的都是Tarjan算法。

这个算法的原理不赘述了。

核心的部分就是，如果u可以到达v，且v在栈中，low[u]=min{low[u],dfn[v]}，如果v不在栈中，low[u]=min{low[u],low[v]}。

我在实现的时候遇到了一个错误，调试了很久，现在记下来。

if (visited[v]==0) {
    tarjan(v);
    LOW[u] = min(LOW[u],LOW[v]);
} else if (inStack[v]==1) {
    LOW[u] = min(LOW[u], DFN[v]);
}

如果v没有被访问过，tarjan搜索（类似于DFS）v。

这里要特别特别注意：

如果v没有被访问过，那么他一定不会在栈中，所以u的LOW等于u和v中LOW较小的一个。

如果v被访问过，那么要分两种情况：

如果v还在栈中，那么说明刚才只是深搜到的v入栈了，那么就u的LOW就是LOW[u]和DFN[v]中较小的一个。

如果v不在栈中了，这里不可以再做LOW[u]=min(LOW[u],LOW[v])，所谓的“如果点v不在栈中，那么LOW[u]=min{LOW[u],LOW[v]}”，前提是v根本不属于任何强连通分量，如果v被访问过，且不在栈中，那么仅有一种可能——当且仅当v被输出过。这是因为v在栈中，要么没有被访问过，要么已经被输出了，但是现在已知v被访问过了，那么v就是属于别的连通分量，被输出了。所以这里的visited[v]==1 && inStack[v]==0是什么都不能做的，我一开始做了一个更新LOW，那就出事了。

小结一下：

visited==0 && inStack==0 : 没有被访问过，递归tarjan，并且更新LOW[u]=min(LOW[u],LOW[v])

visited==0 && inStack==1 : 不可能存在的情况

visited==1 && inStack==0 : 已经处理过这个点了，在其他的强连通分量输出过了，什么都不用做

visited==1 && inStack==1 : 更新LOW[u]=min(LOW[u],DFN[v])

附Tarjan算法核心代码：

/**
 * 求强连通分量SCC，找到就输出
 * @param u 当前检查的顶点编号
 */
void tarjan(int u) {
    DFN[u] = LOW[u] = ++times;
    visited[u] = inStack[u] = 1;
    stack[top++] = u;
    L_NODE* p = head[u];
    while (p!=NULL) {
        int v = p->ver;
        if (visited[v]==0) {
            tarjan(v);
            LOW[u] = min(LOW[u],LOW[v]);
        } else if (inStack[v]==1) {
            LOW[u] = min(LOW[u], DFN[v]);
        }
        p = p->link;
    }
    if (DFN[u] == LOW[u]) {
        printf("Strongly Connected Component %d: ", ++scc);
        int v;
        do {
            v = stack[--top]; 
            printf("%d ",v);
            inStack[v]=0;
        } while (u!=v);
        printf("\n------\n");
    }
}