Visits: 230

硬币

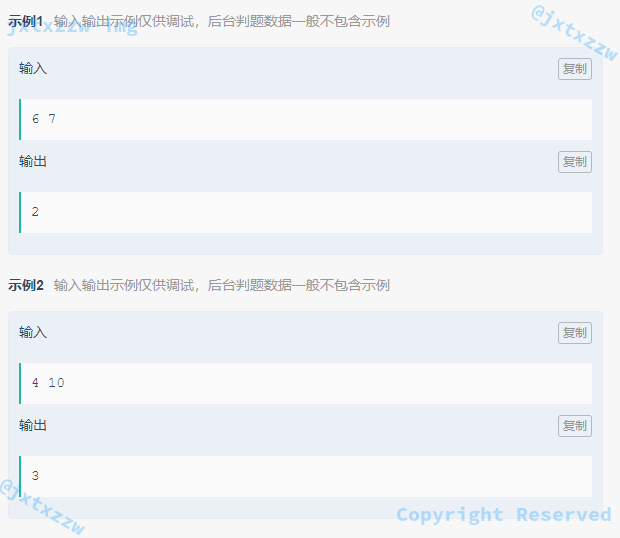
由于硬币是连续的，所以贪心成立。

直接从最大面额的开始支付，直到商品剩余金额小于最大面额，然后用当前不大于商品剩余金额的最大面额开始支付，直到付清。

由于硬币的面额是从 1 开始的，所以一定存在终点。

这与使用现行人民币付款一样，贪心成立。即，10 元、20 元、100 元付款，要求面额最小，一定是先从 100 元的开始支付。

只有在一种情况下，贪心不成立，需要动态规划，那就是硬币的面额是形如 10 元、6 元、1 元，购买 14 元的商品，如果先从 10 元的支付，就剩下 4 元，必须用 4 个 1 元，总共花了 5 个硬币，而如果是 6 + 6 + 1 + 1，就只需要 4 个硬币，因此贪心不成立，只能动态规划。

本题由于硬币从 1 开始，且连续，因此直接贪心。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        if (m < n) {
            System.out.println(1);
        } else {
            int ans = 0;
            int x = n;
            while (m != 0) {
                int num = m / x;
                ans += num;
                m = m - num * x;
                while (x > m)
                    x--;
            }

            System.out.println(ans);
        }
        in.close();
    }

}

奇妙的数列

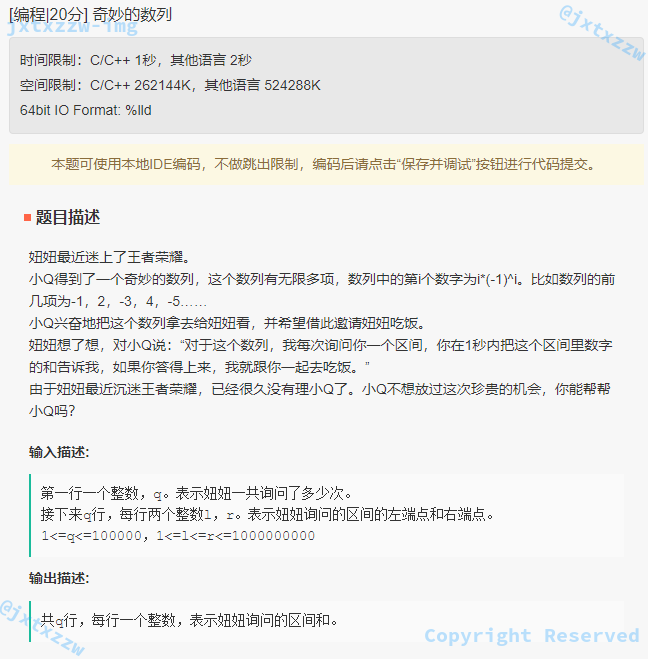
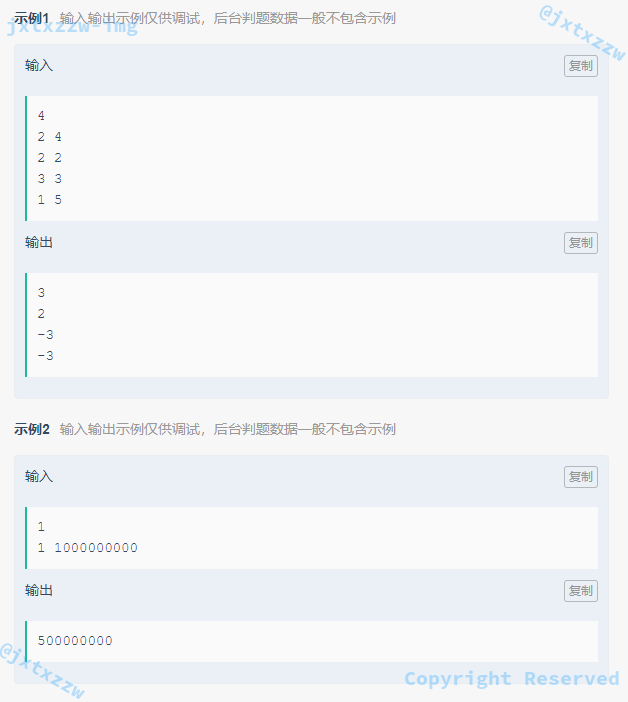
草稿纸上把数列一写，计算差分 f[x] 表示从第 1 个数到第 x 个数的累加，找到规律。

于是，给定区间求区间和，只需要计算差分 $f[R] – f[L]$ 即可。

由于是有规律的，所以直接用公式求，在 $O(1)$ 的时间复杂度得到答案。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        for (int i = 0; i < n; i++) {
            int l = in.nextInt() - 1;
            int r = in.nextInt();
            int L = (l % 2 == 0 ? 1 : -1) * ((l + 1) / 2);
            int R = (r % 2 == 0 ? 1 : -1) * ((r + 1) / 2);
            System.out.println(R - L);
        }
        in.close();
    }

}

石头剪刀布

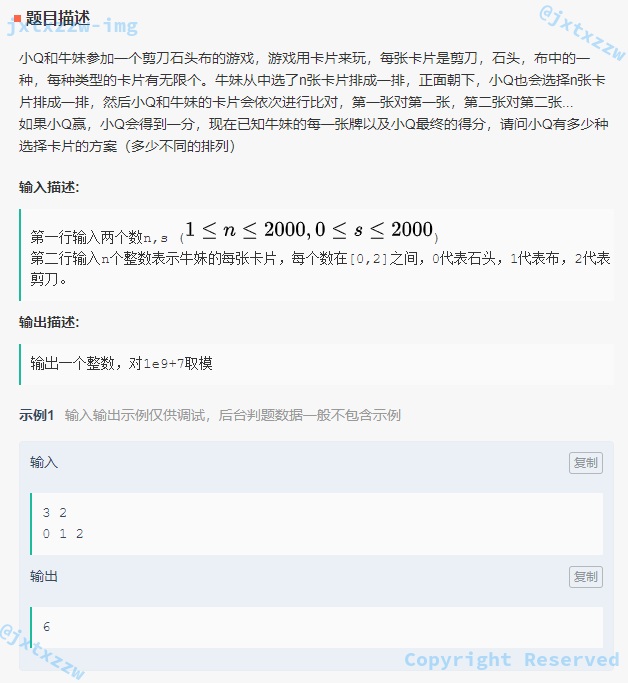
想要得到 $s​$ 分，就必须赢 $s​$ 次，在 $n​$ 张卡牌中找到 $s​$ 张卡片，有 $C_n^s​$ 种可能。

对于找到的这 $s$ 张牌，小Q有且只有一种出牌的方式能得分。

对于剩下的 $n – s$ 张牌，小Q不能赢，那就可以有两种出牌的方式，平局或者输掉，即 $2^{n-s}$ 种可能。

因此，最后的答案就是 $C_n^s \times 2^{n-s}$ 种排列。

答案对 $1E9+7$ 取余数。

事实上题目给出的第 2 行的每张卡牌的信息是多余的，没有用。

由于计算大组合数，所以要考虑计算的效率，以及不能溢出，这里用了 Lucas 定理，其中函数 C(n, m, p) 和 lucas(n, m, p) 表示 $C_n^m$ 对 $p$ 取余后的余数，powMod(n, k, p) 表示 $n^k$ 对于 $p$ 取余后的余数。

有一个小坑，不注意只能通过 80% 的数据——题目没有保证 $s$ 小于 $n$，如果不处理就会死循环。

由于 $n$ 张牌不可能得到大于 $n$ 分，所以一旦出现 $s > n$，就输出 0。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int s = in.nextInt();
        final int p = (int) (1e9 + 7);
        if (s > n)
            System.out.println(0); 
        else
            System.out.println(lucas(n, s, p) * powMod(2, n - s, p) % p);
        in.close();
    }

    static long powMod(long n, long k, long p) {
        long ans = 1;
        while (k != 0) {
            if (k % 2 == 1)
                ans = (ans * n) % p;
            n = (n * n) % p;
            k >>= 1;
        }
        return ans;
    }

    static long C(long n, long m, long p) {
        if (m == 0)
            return 1;
        if (m > n - m)
            m = n - m;
        long up = 1, down = 1;
        for (int i = 1; i <= m; i++) {
            up = (up * (n - i + 1)) % p;
            down = (down * i) % p;
        }
        return up * powMod(down, p - 2, p) % p;
    }

    static long lucas(long n, long m, long p) {
        if (m == 0)
            return 1;
        return C(n % p, m % p, p) * lucas(n / p, m / p, p);
    }

}

气球游戏

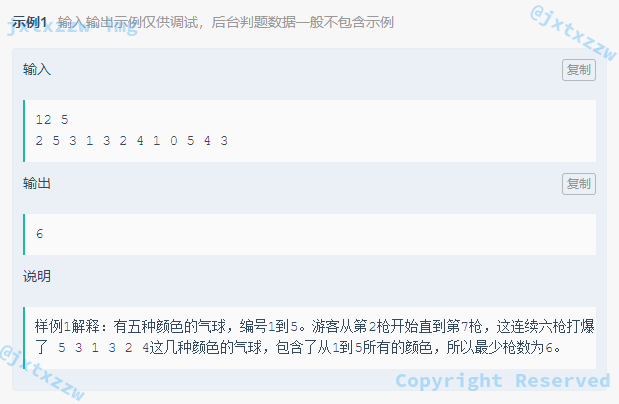
这道题和“洛谷”上面的 1638 逛画展 这题很像。

滑动窗口， 或者说，双指针。

首先确定初始的窗口大小不可能小于 $m$，然后右指针向右移动，直到窗口中包含了所有的颜色气球至少各一个。

之后左指针尝试移动，左指针移动的条件是，当移除最左气球的时候，窗口中仍然保有该颜色气球至少一个，也就是，左指针指向的气球颜色大于 1，左指针移动。

左指针移动的动作是 while 而不是 if，即，如果左指针移动以后指向的那个气球的颜色仍大于 1（不管是刚才那个颜色还是新的颜色）就还是继续移动，如果还是大于 1 就继续移动。

直到左指针移不动了，右指针移动。

窗口滑动的终点是右指针到达尽头。

在整个过程中记录窗口长短的最小值。

需要维护的信息是一个长度为 m 的数组，记录窗口中每个颜色气球有多少个。

在任何条件下，包括初始窗口的确定，如果长度撑满整个数组（右指针到底）了都没能遍历所有颜色气球（即长度为 m 的那个数组中有任何一个元素为 0），输出 -1。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int[] q = new int[n];
        int[] count = new int[m + 1];
        for (int i = 0; i < n; i++) {
            q[i] = in.nextInt();
        }
        int l = 0;
        int r = m - 1;
        for (int i = l; i <= r; i++) {
            count[q[i]]++;
        }
        int min = 0;
        while (!all(count, m)) {
            r++;
            if (r == n) {
                min = -1;
                break;
            }
            count[q[r]]++;
        }
        if (min != -1) {
            min = r - l + 1;
        }
        while (min != -1) {
            while (count[q[l]] > 1) {
                count[q[l]]--;
                l++;
            }
            min = Math.min(min, r - l + 1);
            r++;
            if (r == n)
                break;
            count[q[r]]++;
        }

        System.out.println(min);
        in.close();
    }

    private static boolean all(int[] count, int m) {
        for (int i = 1; i <= m; i++) {
            if (count[i] == 0) {
                return false;
            }
        }
        return true;
    }

}

彩色楼房

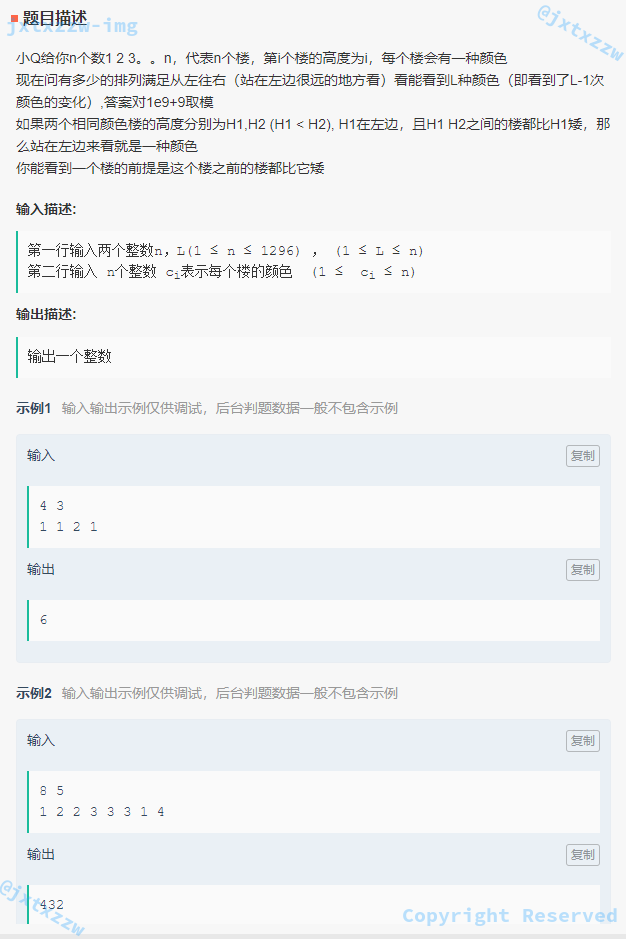
这题不会。

感觉是动态规划。

不过后来时间也来不及了，而且毫无思路，就直接放弃了。

用之前那个组合数的模板，猜了一个 $C_n^L$ 骗分骗了 5% 的测试数据，也好。

后来问了 zerol，他说也不会，感觉是 DP，但是没有思路，不会。并且 zerol 指出，为什么猜 $C(n, L)$ 呢，要猜也猜 $ n! $ 之类的。

不过可以肯定的是，这一题的第 2 行，是真的有用的了。