什么是逻辑回归

逻辑回归又称为逻辑回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。

样本的 $x$ 包括很多特征向量，$y$ 标签多数是 $2$ 个值，例如，“是”或者“否”。

然后通过逻辑回归分析，可以得到各个自变量的权重，从而可以大致了解到底哪些因素是影响结果的关键因素。

同时根据该权值可以根据将各个特征向量进行一定的计算得到一个预测值，来预测“是”或者“否”的概率。

逻辑回归用来分类

逻辑回归，虽然名字里带“回归”，但是它实际上是一种分类方法，用于二分类问题。

逻辑回归的解题步骤，与线性回归是类似的。

线性回归不能用来做分类，是因为对于 $p(y=1)=w_0+w_1 x_1+w_2 x_2+\ldots+w_n x_n$

• $p$ 的取值范围是 $[0,1]$，而等式右边是 $(-\infty,+\infty)$
• 实际中很多问题，概率 $p$ 与自变量并不是直线关系

我们希望将 $w_0+w_1 x_1+w_2 x_2+\ldots+w_n x_n$ 经过某种变换以后，变成一个可以用来表示 $p(y=1)$ 的值。

首先，要找一个合适的预测函数， $h$，它用来预测输入数据的判断结果。

显然，为了完成二分类的目标，该函数的输出必须是两个值，分别代表两个类别。

$\displaystyle P(y=1|x)=\frac{e^{\theta^{T}x}}{1+e^{\theta^{T}x}}=\frac{1}{1+e^{-\theta^{T}x}}$

$\displaystyle P(y=0|x)=\frac{1}{1+e^{\theta^{T}x}}$

然后，构造一个损失函数，该函数表示预测的输出 $h$ 与训练数据类别 $y$ 之间的偏差，可以是二者之间的差 $h-y$ 或者是其他的形式。

综合考虑所有训练数据的损失，将损失累加求和或者求平均，记为 $J(\theta)$ ，表示所有训练数据预测值与实际类别的偏差。

显然，$J(\theta)$ 函数的值越小表示预测函数越准确，所以这一步需要做的是找到 $J(\theta)$ 函数的最小值。

找函数的最小值有不同的方法，实现时有的是梯度下降法。

Sigmoid 函数

由于 $h$ 必须只产生两个值，所以通常会利用 Sigmoid 函数，函数形式为 $\displaystyle \frac{1}{1+e^{-x}}$。

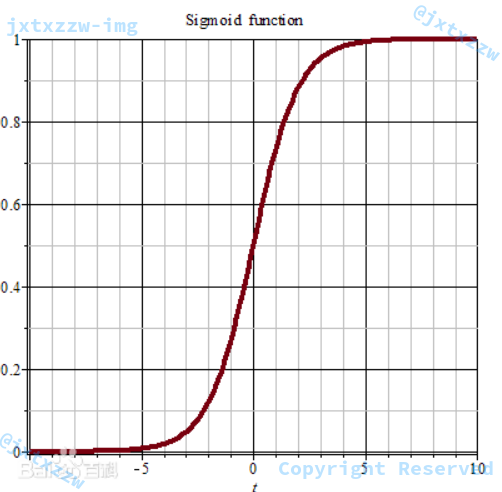
这样，不管 $h$ 函数最终计算的值是多少，都可以映射到 $[0,1]$ 区间。

且观察图像可知，对于多数情况来说，可以认为 $h$ 函数经过 Sigmoid 函数之后，值或者是 $1$，或者是 $0$，不会出现其他的值。

更一般地，可以对二分类的标准定义为，大于 $0.5$ 为一个分类，否则为另一个分类。

如果将 Sigmoid 函数运用在神经网络等训练模型中，在实际的代码中，可以给 $x$ 增加了一个响应 RESPONSE。

这是因为 $x$ 的取值负的越小，或者正的越大的时候，就越是逼近 $0$ 或 $1$（饱和区）。如果在饱和区，由于反向传播是 Sigmoid 函数的导数，当逼近饱和区时，因为曲线变得平缓，斜率就趋近于 $0$。这样对于得到的权重变化就会非常非常小，也趋近于 $0$， 也就是几乎达不到演化神经网络的目的（因为权重基本上没什么变化，就没有调整权重的意义了）。

当然这个技巧在这里并没有什么用……

损失函数

$\displaystyle J(\theta)=-m^{-1}l(\theta)=-m^{-1}\sum_{i}^{m}{[y^{(i)} \ln h_{\theta}(x^{(i)})+(1-y^{(i)}) \ln ( 1-h_{\theta}(x^{(i)}) )]}$

随机梯度下降

• 初始化最初解
• 循环直至收敛

$\displaystyle \theta_j = \theta_j – \alpha \frac{\partial{J}}{\partial{\theta_j}}=\theta_j-\alpha(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$

事件发生与不发生的概率的比值$\displaystyle odds=\frac{P(y=1|x)}{1-P(y=1|x)}=\frac{p}{1-p}$

对数线性模型 $logit(p)=\ln⁡(odds)= θ^Tx$

逻辑回归进行多分类

如上文，逻辑回归只能用来做二分类。

所以如果需要使用逻辑回归来进行多分类，就需要使用 SoftMax。

简单说，就是，对于需要分类的 $K$ 个分类，分别求出属于第 $K_i$ 个分类的概率大小。

于是在这 $K$ 个概率中，选择最大的那个，作为最后的分类结果。

SoftMax

显然，我们需要找到的这个函数，需要保证对于一个多项式 $w_0+w_1 x_1+w_2 x_2+\ldots+w_n x_n$，它都能将其映射到区间 $[0,1]$之间。且特别地，所以这个函数还需要保证，所有概率的和，必须严格等于 $1$。

在数学，尤其是概率论和相关领域中，SoftMax 函数，或称归一化指数函数，是逻辑函数的一种推广。

它能将一个含任意实数的 $K$ 维向量 ${\displaystyle \mathbf {z} }$ 压缩到另一个 $K$ 维实向量 ${\displaystyle \sigma (\mathbf {z} )}$ 中，使得每一个元素的范围都在${\displaystyle (0,1)}$ 之间，并且所有元素的和为 $1$。

该函数通常以下面的形式给出：

${\displaystyle \sigma_{j}={\frac {e^{z_{j}}}{\sum {k=1}^{K}e^{z{k}}}}}$

SoftMax 函数实际上是有限项离散概率分布的梯度对数归一化。

因此，SoftMax 函数在包括多项逻辑回归，多项线性判别分析，朴素贝叶斯分类器和人工神经网络等的多种基于概率的多分类问题方法中都有着广泛应用。

特别地，在多项逻辑回归和线性判别分析中，函数的输入是从 $K$ 个不同的线性函数得到的结果，而样本向量 $x$ 属于第 $j$ 个分类的概率为：

${\displaystyle P={\frac {e^{\mathbf {x} ^{\mathsf {T}}\mathbf {w} _{j}}}{\sum _{k=1}^{K}e^{\mathbf {x} ^{\mathsf {T}}\mathbf {w} _{k}}}}}$

这可以被视作 $K$ 个线性函数 ${\displaystyle \mathbf {x} \mapsto \mathbf {x} ^{\mathsf {T}}\mathbf {w} _{1},\ldots ,\mathbf {x} \mapsto \mathbf {x} ^{\mathsf {T}}\mathbf {w} _{K}}$ SoftMax 函数的复合${\displaystyle \mathbf {x} ^{\mathsf {T}}\mathbf {w} }$。

SoftMax 针对多类分类，输出的是每一个分类的概率。

特别的，当类别数 $K=2$ 时，SoftMax 回归退化为 Logistic 回归。

这表明 SoftMax 回归是 Logistic 回归的一般形式。

$ \begin{align} h_\theta&= \frac{1}{ e^{\theta_1^Tx} + e^{ \theta_2^T x^{(i)} } } \begin{bmatrix} e^{ \theta_1^T x } \ e^{ \theta_2^T x } \end{bmatrix} \end{align} $

推导过程从略，可参考《机器学习》（周志华），或 http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92 。

选择哪种分类器

那么，对于特定的问题，到底是使用 SoftMax 分类器呢，还是使用逻辑回归算法建立 $K$ 个独立的二元分类器呢？

斯坦福大学的Wikipedia上给出的建议是：

如果你在开发一个音乐分类的应用，需要对 k 种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？

这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为 5。）

如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。

现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？

在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

引自 http://ufldl.stanford.edu

对于本次作业来说，鸢尾花分类，以及红酒品质分类，是互斥的。即，某个数据不可能同时输出多个类别。

因此更加适合选择 SoftMax 回归分类器。

核心代码

首先假设已经存在一个 $K$ 行 $N$ 列的矩阵，其中 $K$ 表示需要进行的是 $K$ 分类，$N$ 表示数据集的每条记录有 $N$ 个特征向量。

特别的，如果需要加上常数项，那么这是一个 $K$ 行 $N+1$ 列的矩阵。

之后对于每一个给定的数据记录，都可以通过 $\displaystyle P(K_i) = w_{i_0} + w_{i_1} \times x_1 + w_{i_2} \times x_2 + \ldots + w_{i_n} \times x_n$ 求出这条记录属于第 $K_i$ 个分类的概率。

进行 $K$ 次计算以后，就得到了这个记录属于每一个分类的可能性大小，那么，简单地取概率最大的那个 $P(K_i)$ 就认为是属于这个分类的。

基于这样的思路，就可以写出预测函数。

public double predict(ArrayList<Double> x) {
    double[] p = new double[K];
    for (int i = 0; i < K; ++i) {
        for (int j = 0; j < DIM; ++j) {
            p[i] += x.get(j) * weight[i][j];
        }
    }
    int idx = 0;
    double tmp = p[idx];
    for (int i = 0; i < K; ++i) {
        if (p[i] > tmp) {
            tmp = p[i];
            idx = i;
        }
    }
    return idx;
}

代码中，x是需要预测的数据集，K是需要在多少个分类中进行预测，DIM是数据集的维度，idx是最后预测的结果属于哪一个分类。

for (int i = 0; i < K; ++i)
    for (int j = 0; j < DIM; ++j)
        p[i] += x.get(j) * weight[i][j];

这个循环，就是计算出了 $\displaystyle P(K_i) = w_{i_0} + w_{i_1} \times x_1 + w_{i_2} \times x_2 + \ldots + w_{i_n} \times x_n$。

之后通过一个简单的遍历，找到最大值，并取最大值的下标作为分类预测的结果。

 for (int i = 0; i < K; ++i)
     if (p[i] > tmp) {
         tmp = p[i];
         idx = i;
     }

所以，现在问题的关键就变成了，如何求出权重矩阵 $W$，即上面代码中的 $weight[][]$。

先写大的框架。

对于一组向量 $x$ 和一个标签 $y$，首先计算对每个分类的偏导。

for (int i = 0; i < K; ++i)
    partialDerivative.add(calculatePartialDerivative(i, x, y));

求出了 $K$ 个偏导以后，更新权重矩阵。

具体来说，对于第 $i$ 个分类的偏导partialDerivative[i]，这是一个 $1$ 行 $N$ 列的矩阵（加上常数项就是 $N+1$ 列），对这个矩阵的每一个向量乘上一个学习率learningRate得到一个新的矩阵，然后用原来的weight[i]减去这个矩阵作为新的weight。

相当于是，我用当前的权重算了一些东西出来，然后发现不对，有偏差、有损失。

那么这个损失就应该是要被避免的，所以权重矩阵应该往损失减少的地方去。

去多少呢？学习率越大，就去的越多，表示纠正自己的力度越大，学习率越小，就稍微改一改。

由于 Java 不能直接做矩阵和常数相乘、矩阵与矩阵相减，所以要写一个循环来做。

for (int i = 0; i < K; ++i) 
    for (int j = 0; j < DIM; j++) 
        weight[i][j] -= learningRate * partialDerivative.get(i).get(j);

如果是 Python 的话就简单了：

for k in range(K):
    w[k] -= lr * pd[k]

下面就要实现partialDerivative()这个函数了。

这个是在计算第 $k$ 类的参数梯度。

在此之前，先写两个辅助函数。

一个是计算指数的，这个函数是将某个分类的 $weight[i]$ 矩阵与 $x$ 相乘、累加，并返回其自然指数的值。

如果记 $weight[]$ 为 $\theta$，那么 $weight[i]$ 就是 $\theta_i$，这里求的就是 $\theta_i ^{T} x$。

用 Python 来表达，就是：

theta_l = self.w[l]
product = np.dot(theta_l,x)

在 SoftMax 函数中，这一部分被表达为 $\displaystyle e^{\theta_j^{T} x^{(i)}}$，因此，最后返回的结果还需做一次自然指数，即返回exp(product)。

$\displaystyle e^{\theta_j^{T} x^{(i)}}$，可以直接用 Python 的 numpy 的dot()，或者用 numpy 的矩阵转置先求出 $\theta_j.T$ 再求。

如果自己实现，就是遍历所有的向量，累乘、累加。

double sumOfProduct = 0;
for (int i = 0; i < DIM; ++i) {
    double xx = x.get(i);
    double ww = w[i];
    sumOfProduct += xx * ww;
}
return Math.exp(sumOfProduct);

之后对于公式中的 $\displaystyle \frac{e^{\theta_j^{T} x^{(i)}}}{\displaystyle \sum_{l=1}^{k} e^{\theta_l^{T} x^{(i)}}}$，由于分子、分母的 $e^{\theta_j^{T} x^{(i)}}$ 已经可以通过调用calculateExp(ArrayList<Double> x, double[] w)来计算了，所以，只需要对分母进行累加即可。

private double calculateProbability(ArrayList<Double> x, int k) {
    double numerator = calculateExp(x, weight[k]);
    double denominator = 0;
    for (int i = 0; i < K; ++i) {
        denominator += calculateExp(x, weight[i]);
    }
    return numerator / denominator;
}

这里，分子numerator直接调用calculateExp(x, weight[k])，$k$ 是当前的类别。

分母denominator就是calculateExp(x, weight[i])的累加，$i$ 从 $0$ 到 $k-1$。

对于 Python，求分母甚至只需要一句话：

denominator = sum([calculateExp(x, i) for i in range(K)])

那么，求概率就是：

double probability = calculateProbability(x, k);

有了这两个函数，下面进行偏导的计算就好办了。

$\textstyle 1{\cdot}$是示性函数，其取值规则为，$\textstyle 1{值为真的表达式}=1$。

所以，$\begin{align} J= – \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left{y^{(i)} = j\right} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right] \end{align} $ 式中的 $1\left{y^{(i)} = j\right} $，就可以表示为：

double characteristic = k == y ? 1.0 : 0.0;

如果我们忽略这里的常系数，例如 $-\frac{1}{m}$ 以及 $\log()$，那么， $1\left{y^{(i)} = j\right} \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} $，就可以表示为 characteristic * probability。

下面考虑，对于characteristic，这是我期望得到的结果，而我实际算出来的结果是probability。

直接运用公式，偏导为：

- x * (characteristic - probability) + weightDecay * w[k]

这里 $x$ 和 $w[k]$ 都是包含了 $N$ 个向量的矩阵。

double delta = (characteristic - probability);
for (int i = 0; i < x.size(); i++) {
    double xx = x.get(i);
    xx *= delta;
    pd.add(weightDecay * weight[k][i] - xx);
}

下面对于每一个 $k$ 都这么求偏导。

for (int i = 0; i < K; ++i)
    partialDerivative.add(calculatePartialDerivative(i, x, y));

partialDerivative = [calculatePartialDerivative(k, x, y) for k in range(K)]

最后，更新权重矩阵。

for (int i = 0; i < K; ++i) 
    for (int j = 0; j < DIM; j++) 
        weight[i][j] -= learningRate * partialDerivative.get(i).get(j);

全部写完了，我把它封装成了一个类，SoftMaxRegression。

增加了必要的构造器，例如：

public SoftMaxRegression(double learningRate, double weightDecay, int k, int dIM, int iTERATION_TIMES) {
    this.learningRate = learningRate;
    this.weightDecay = weightDecay;
    K = k;
    DIM = dIM;
    ITERATION_TIMES = iTERATION_TIMES;
    weight = new double[K][DIM];
}

以及一些辅助函数，例如：

public double[][] getWeight() {
    return weight.clone();
}

具体看源代码。

对于数据的读入，与前几次是大同小异的，我不赘述了，我还是写了一个类来处理数据的读入。

例如核心部分有：

for (int i = 0; i < len - 1; i++) {
    feature.add(Double.valueOf(ss[i]));
}
feature.add(CONSTANT_TERM);
features.add(feature);
double label = Double.valueOf(ss[len - 1]);
labels.add(label);

具体看源代码。

这里需要说明的是，我增加了一个常数项，所以，向量的维度是 $N+1$。

for (int i=0;i<len - 1;i++) {
    feature.add(Double.valueOf(ss[i]));
}
feature.add(CONSTANT_TERM);
features.add(feature);

最后的main()函数就相对简单了。

DataSet train = new DataSet(new File("train.txt"), true);
DataSet test = new DataSet(new File("test.txt"), false);
ArrayList<ArrayList<Double>> features = train.loadFeatures();
ArrayList<Double> labels = train.loadLabels();
final int K = new HashSet<Double>(labels).size();
final int DIM = features.get(0).size();
final double learningRate = 0.01;
final double weightDecay = 0.01;
final int ITERATION_TIMES = 100000;

在处理了一大堆的常数定义和数据读入后，直接调用train()来训练，然后输出权重矩阵。

SoftMaxRegression smr = new SoftMaxRegression(learningRate, weightDecay, K, DIM, ITERATION_TIMES);
smr.train(features, labels);

double[][] w = smr.getWeight();
System.out.println(Arrays.deepToString(w));

之后依次预测，并输出结果。

features = test.loadFeatures();
for (int i = 0; i< features.size();++i) {
    int result = (int) smr.predict(features.get(i));
    String label = "";
    switch (result) {
        case 0:
            label = "Iris-setosa";
            break;
        case 1:
            label = "Iris-versicolor";
            break;
        case 2:
            label = "Iris-virginica";
            break;
    }
    System.out.println(label);
}

运行结果

对于鸢尾花数据集，我的准确率是 $100\%$。

需要说明的是，本来我用的是：

int number = features.size();
for (int t = 0 ; t < ITERATION_TIMES;t++) {
    for (int index = 0; index < number;index++) {
        ArrayList<Double> x = new ArrayList<Double>();
        x.addAll(features.get(index));
        double y = labels.get(index);
        // DO SOMETHING ...
    }
}

但是发现这样会过度拟合，导致准确率只有 $70\%$。

所以我采取了以下方案：

int number = features.size();
for (int t = 0 ; t < ITERATION_TIMES;t++) {
    int index = (int) (Math.random() * number);
    ArrayList<Double> x = new ArrayList<Double>();
    x.addAll(features.get(index));
    double y = labels.get(index);
    // DO SOMETHING ...
}

这样就准确率到了 $100\%$。

对于红酒品质的分级，因为我的代码封装的比较好，所以根本不需要关心，数据集有多少条数据、每条数据有多少个维度……都不需要关心，直接用，都能正确处理。

唯一需要修改的，就是把鸢尾花的标签的字符串与数值相互映射的部分去掉，因为红酒分级这里所有的标签本来就是数值了。

除此而外，就是参数优化了，调整

• double learningRate
• double weightDecay
• int iTERATION_TIMES