Visits: 107

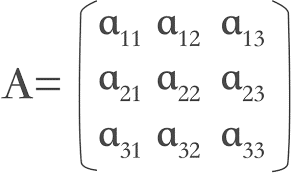
计蒜客 矩阵查询

题目描述

给出 $N \times N$ 的矩阵 $A$，初始时均为 $0$。

我们需要支持两种操作：

$ C \ x_1 \ y_1 \ c $，表示 $(x_1, y_1)$ 上的元素加上 $c$。

$(1 \leq x_1, y_1 \leq N, 1 \leq c \leq 100)$

$Q \ x_1 \ y_1 \ x 2 \ y_2$，查询子矩阵元素之和。

$(1 \leq x_1 \leq x_2 \leq N, 1 \leq y_1 \leq y_2 \leq N)$

样例

样例输入

第一行两个整数 $N,Q(1\leq N\leq 1000, 1\leq Q\leq 50000)$。接下来 $Q$ 行，每行一个操作。

3 5
C 1 1 3
Q 1 1 2 3
C 1 2 1
C 2 1 1
Q 1 1 2 3

样例输出

对于每个询问操作，一行一个整数，表示矩阵的和。

3
5

算法与数据结构

树状数组

题解

裸的树状数组。子矩阵的和只需要使用四个矩阵的容斥就可以完成。

完整代码

#include <bits/stdc++.h>

using namespace std;

int n = 0;
const int MAX_N = 1007;
int C[MAX_N][MAX_N] = {{0}}; // 树状数组 C

int lowBit(int x) {
    return x & -x; // return x & (x ^ (x - 1))
}

// 查询
int sum(int i, int j){
    int res = 0;
    for(int x = i; x; x -= lowBit(x))
        for(int y = j; y; y -= lowBit(y))
            res += C[x][y];
    return res;
}

// 修改
void change(int i, int j, int delta){
    for(int x = i; x < MAX_N; x += lowBit(x)) {
        for (int y = j; y < MAX_N; y += lowBit(y)) {
            C[x][y] += delta;
        }
    }
}

// 子矩阵的操作只需要使用 4 个树状数组矩阵的容斥就可以解决

// 子矩阵查询
int subSum(int x1, int y1, int x2, int y2) {
    return sum(x2, y2) - sum(x1 - 1, y2) - sum(x2, y1 - 1) + sum(x1 - 1, y1 - 1);
}

int main() {
    int t;
    scanf("%d%d", &n, &t);
    for (int i = 0; i < t; i++) {
        char op;
        scanf("\n%c", &op);
        if (op == 'C') {
            int x, y, c;
            scanf("%d%d%d", &x, &y, &c);
            change(x, y, c);
        } else {
            int x1, y1, x2, y2;
            scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
            printf("%d\n", subSum(x1, y1, x2, y2));
        }
    }

    return 0;
}