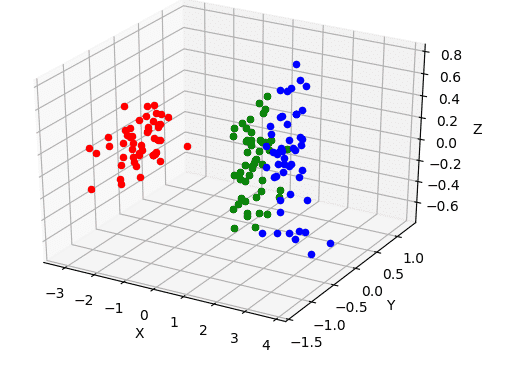
使用 PCA 对数据集进行降维操作

定义

PCA 是一种数据降维的常用方法，并且降维的同时去除了原始数据的噪声。

通过一个正交转换把可能线性相关的变量转换为几乎线型无关的变量（这些变量称作主成分）。

主成分的数量比原来的变量数量更少或者一致。

为什么要用 PCA

减少特征。

PCA 可以解决如下问题：

降维——删掉冗余的特征，且不会丢失太多的信息。

需要解决的关键

• 要删除哪一个特征损失的信息才最小
• 根本不是单纯的删除几个特征，而是通过某种变换将原始数据中的特征减少，又使得丢失的信息最少
• 如何度量丢失信息的多少
• 如何决定具体的降维步骤

PCA 运算的推导过程

向量的表示与基变换

从略。

基变换的矩阵表示

从略。

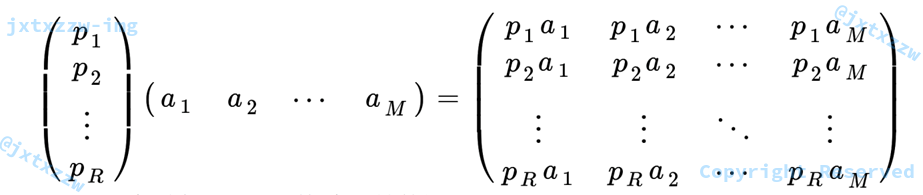
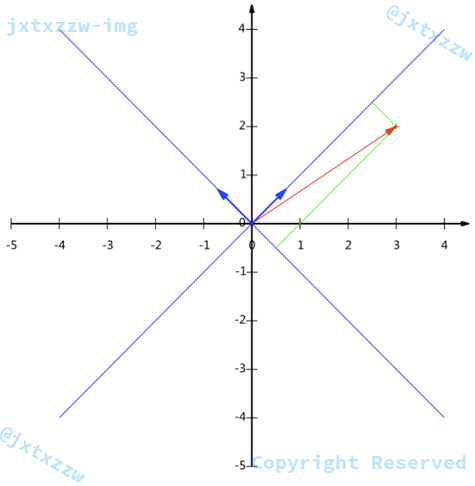
如何选择基才能最大程度的保留原有的信息

投影后的投影值尽可能的分散。

我们希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述。

一个特征的方差可以看做是每个元素与特征均值的差的平方和的均值。

从直观上说，让两个特征尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个特征不是完全独立，必然存在重复表示的信息。

用两个特征的协方差表示其相关性。

当协方差为0时，表示两个特征完全独立。

为了让协方差为0，我们选择第二个基时只能在与第一个基正交的方向上选择。

因此最终选择的两个方向一定是正交的。

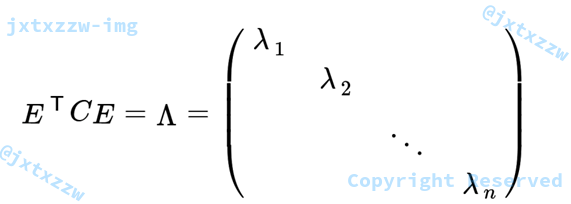
降维的目标

将一组 $N$ 维向量降为 $K$ 维（ $K$ 大于 $0$，小于 $N$），其目标是选择 $K$ 个单位（模为 $1$）正交基，使得原始数据变换到这组基上后，各特征两两间协方差为 $0$，而特征的方差则尽可能大（在正交的约束下，取最大的 $K$ 个方差）。

得到降维后的矩阵

$P$ 是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是 $C$ 的一个特征向量。如果设 $P$ 按照特征值的从大到小，将特征向量从上到下排列，则用 $P$ 的前 $K$ 行组成的矩阵乘以原始数据矩阵 $X$，就得到了我们需要的降维后的数据矩阵 $Y$。

算法步骤

1. 将原始数据按行组成 $m$ 行 $n$ 列矩阵 $X$。
2. 将 $X$ 的每一列（代表一个属性字段）进行零均值化。
3. 求出协方差矩阵 $\displaystyle C=\frac{1}{m-1}{X^T}{X}$。
4. 求出协方差矩阵的特征值及对应的特征向量。
5. 将特征向量按对应特征值的大小，从左到右按列排列成矩阵，取前 $k$ 列组成矩阵 $P$。
6. 此时矩阵 $P$ 是 $n$ 行 $k$ 列的矩阵，矩阵 $X$ 是 $m$ 行 $n$ 列的矩阵。
7. $\displaystyle Y=X \times P$即为降维到 $k$ 维后的数据。

代码

Python代码

import numpy as np


# 分词，以逗号分隔，并把数据转换成浮点数
def get_fv(ss):
    fv = []
    ss = ss.strip().split(',')
    for s in ss:
        fv.append(float(s))
    return fv


m, n, k = map(int, input().strip().split())

fv = []  # 存放向量
fv_sum = []  # 存放每一个属性的和，为后面计算属性均值
for j in range(n):
    fv_sum.append(0)
for i in range(m):
    # 遍历m条记录，加入矩阵，并对每一个属性分别求和累加
    fv_i = get_fv(input())
    fv.append(fv_i)
    for j in range(n):
        fv_sum[j] += fv_i[j]

for j in range(n):
    fv_sum[j] /= m  # 计算平均数
for i in range(m):
    for j in range(n):
        fv[i][j] -= fv_sum[j]  # 去均值化
X = np.mat(fv)
# 以上两个步骤，可以直接用numpy实现
# mean = np.mean(mat, axis=0)
# mat = mat - mean


C = X.T * X * (1/(m-1))  # 求协方差矩阵
# 注意这里是除以(m - 1)，助教PPT写错了
# 上面这个步骤，可以直接用numpy实现
# C = np.cov(X.T)

f_val, f_vec = np.linalg.eig(C) # 求特征值和特征向量
f_val_argsorted = np.argsort(f_val) # 对特征值的下标排序
# 一般的排序，都是对元素排序，例如，[2, 1, 3]排序后就是[1, 2, 3]
# 而argsort是对下标排序，排序后的结果是[1, 0, 2]，意思是，这三个数分别是第2小、最小、最大
# 于是可以利用这个结果，直接取出最大的k个特征值和特征向量

idx = []
for i in range(len(f_val_argsorted) - 1, len(f_val_argsorted) - k - 1, -1):
    idx.append(f_val_argsorted[i])
for i in idx:
    print(f_val[i], end=' ')  # 输出特征值
print()
p = []
for j in range(n):
    p_i = []
    for i in idx:
        print(f_vec[j, i], end=' ')  # 输出特征向量
        p_i.append( f_vec[j, i])
    print()
    p.append(p_i)

# Y = X * P，得到降维后的矩阵，并输出
P = np.mat(p)
Y = X * P
for i in range(m):
    for j in range(k):
        print(Y[i, j], end=' ')
    print()
print()

实现技巧

1. 去均值化首先求出每个属性的均值，然后遍历相减

   可以直接用numpy.mean()

   for j in range(n):
      fv_sum[j] /= m  # 计算平均数
   for i in range(m):
      for j in range(n):
          fv[i][j] -= fv_sum[j]  # 去均值化
   X = np.mat(fv)
   # 以上两个步骤，可以直接用numpy实现
   # mean = np.mean(mat, axis=0)
   # mat = mat - mean

2. 求协方差矩阵$\displaystyle C=\frac{1}{m-1}{X^T}{X}$

   可以直接用numpy.cov()

   C = X.T * X * (1/(m-1))  # 求协方差矩阵
   # 注意这里是除以(m - 1)，助教PPT写错了
   # 上面这个步骤，可以直接用numpy实现
   # C = np.cov(X.T)

3. 取前 $k$ 大的特征值和特征向量一般的排序，都是对元素排序，例如，[2, 1, 3]排序后就是[1, 2, 3]

   而argsort()是对下标排序，排序后的结果是[1, 0, 2]，意思是，这三个数分别是第2小、最小、最大

   于是可以利用这个结果，直接取出最大的k个特征值和特征向量

OJ测评结果截图

绘制出降维后的数据分布散点图

步骤说明

已经求出了降维后的矩阵

且由上面的代码可知，降维后的矩阵的每条记录的顺序是按照原顺序输出的

那么，由原数据，就可以得到标签字段

下面，根据每一个标签，对数据着色

例如，我将某数据集降维成二维，得到的矩阵是

$\displaystyle\left[\begin{array}{cc}
​ 1 & 6 \\
​ 7 & 9\\
​ 9 &5 \\
\end{array}\right]$

而这三条记录对应的标签分别是：$A$、$B$、$A$

不妨假设我用绿色表示 $A$、用蓝色表示 $B$，那么，我只要将点 $(1,6)$ 和 $(9,5)$ 着色为绿色、将点 $(7,9)$ 着色为蓝色

之后生成图像就可以了

核心代码

设置着色的部分，就是一个遍历，然后用 if 条件句判断，是哪个标签，就设置什么颜色

for i in range(m):
    fv_i = fv[i]
    label = L[i]
    if (label == "Iris-setosa"):
        color = 'r'
    elif (label == "Iris-versicolor"):
        color = 'g'
    elif (label == "Iris-virginica"):
        color = 'b'
    xi, yi, zi = fv_i[0], fv_i[1], fv_i[2]

对于降维到二维，也是类似的

xi, yi = fv_i[0], fv_i[1]

输出，可以直接用matplotlib包

matplotlib.pyplot.figure().add_subplot()

对于三维可以设置projection='3d'

例如设置三维空间的某个点的颜色

graphic.scatter(xi, yi, zi, c=color)

最后设置一下坐标轴set_xlabel('X')等等信息，比如标题啊什么的

然后保存plt.savefig("file_name")

导出的图

一维

都夹杂在一起，没有实际应用意义。

图略。

二维

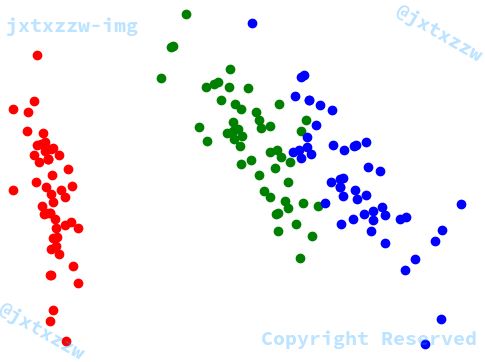
三维

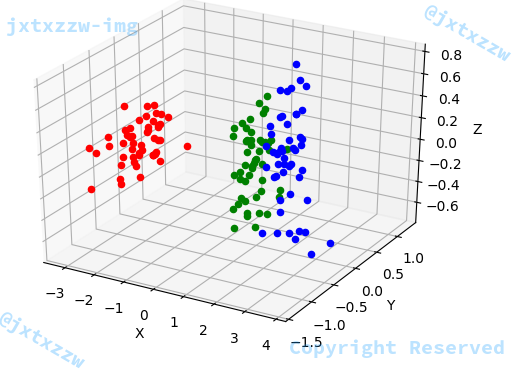
PCA

如果直接使用SKLearn的库函数，那么可以一键获得降维后的矩阵，以及生成图片

pca = PCA(n_components=2)

其中n_components就是降维到多少维度，也就是本题中的 $k$ 值

reduced_X = pca.fit_transform(X)

得到的就是降维后的矩阵

数据集可以是直接用

from sklearn.datasets import load_iris
data = load_iris()

也可以手动读入、处理，然后作为矩阵参数传入

得到矩阵以后画图的部分是类似的

可以指定不同的类别用不同的形状

marker='x'

例如下面这张就是调用 PCA 得到的降维矩阵生成的

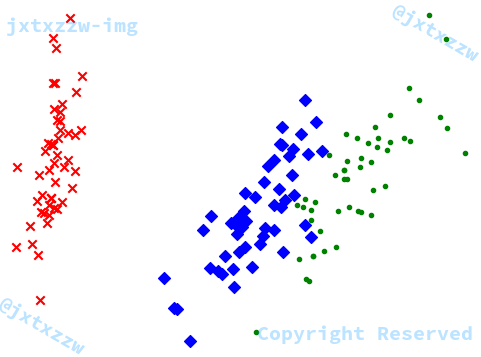
可以发现，这与我们自己生成的图片是类似的

只是方向正好反了一下

但是显然，不管方向怎么样，都应该认为是正确的解

因此，我在设计 $OJ$ 的 $Checker$ 的时候，就考虑了这件事情

你输出的数字可以是整数，也可以是浮点数，浮点数你可以保留到小数点后任意位数，但是请确保精度在 10−4以上。

不关心降维后数据集的方向（即正负号），判题系统会对所输出的降维矩阵的数值取绝对值后判断。

Behind the scene

Statement

Description

请你使用PCA方法对给定的数据集进行降维操作，并输出降维后的矩阵以及必要的信息。

1. 将原始数据按行组成 $m$ 行 $n$ 列矩阵 $X$。
2. 将 $X$ 的每一列（代表一个属性字段）进行零均值化。
3. 求出协方差矩阵 $\displaystyle C=\frac{1}{m-1}{X^T}{X}$。
4. 求出协方差矩阵的特征值及对应的特征向量。
5. 将特征向量按对应特征值的大小，从左到右按列排列成矩阵，取前 $k$ 列组成矩阵 $P$。
6. 此时矩阵 $P$ 是 $n$ 行 $k$ 列的矩阵，矩阵 $X$ 是 $m$ 行 $n$ 列的矩阵。
7. $\displaystyle Y=X \times P​$即为降维到 $k​$ 维后的数据。
8. 你需要输出的是， $k$ 个从大到小排列的特征值、矩阵 $P$、矩阵 $Y$。

你有最多 $15$ 秒的时间，和 $512$ M 的内存。

Input

第 $1$ 行是 $3$ 个正整数 $m,n,k$。$m$ 表示数据集有 $m$ 条记录，$n$ 表示每条记录有 $n$ 个字段, $k$ 表示你需要将 $n$ 维的数据降维到 $k$ 维。

下面 $m$ 行是每行一个记录，包括由,分隔的 $n$ 个字段，这些字段都是特征向量，数据类型是浮点数，记录不包括标签字段。

数据保证，$m, n, k$ 都是正整数，且保证，$k \lt n$。

Output

你需要输出 $1 + n + m$ 行， 每行是 $k$ 个用空格分隔的数字。

第 $1$ 行是 $k$ 个以空格分隔的数，表示你选取的（即最大的） $k$ 个特征值。

第 $2$ 行到第 $1+n$ 行，每行是 $k$ 个以空格分隔的数，这 $n \times k$ 个数表示的是你选取的特征向量。

从第 $n+2$ 行开始，你应该输出 $m$ 行，表示降维后的每一条记录。每行 $k$ 个字段，用空格分隔，每个字段是一个数字。

输出第 $1$ 行的时候，请按照特征值从大到小排列。

下面你选取的 $n$ 行 $k$ 列的特征向量矩阵，每一列应该是对应第 $1$ 行的特征值的向量。

最后的降维后的矩阵，从上到下是原数据集的顺序，从左到右是特征值从大到小排列的 $k$ 个降维后的向量。即，应该是由数据集 $m \times n $ 的矩阵，和 $n \times k$ 的矩阵相乘，得到的 $m \times k$ 的顺序。

Examples

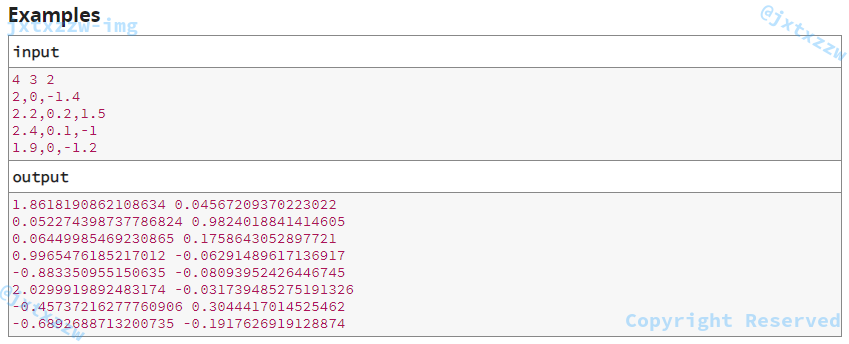
Note

你需要使用PCA方法对数据进行降维，你可以使用任何你喜欢的编程语言来实现数据的读入以及矩阵的运算。

特别需要指出的是，对于 Python ，你不可以使用 SciKit-Learn 库。如果你需要使用 numpy 来简化矩阵的运算，你可以使用这个包，如果你使用了 numpy 那么请使用 Python(SCI) 提交而不是 Python3 。

记录和字段的顺序，请严格按照输入的顺序。

你输出的数字可以是整数，也可以是浮点数，浮点数你可以保留到小数点后任意位数，但是请确保精度在 $10^{-4}$以上。

不关心降维后数据集的方向（即正负号），判题系统会对所输出的降维矩阵的数值取绝对值后判断。

标准结果是唯一的测评标准。

有多组测试数据，测评会测评所有组的数据，而不是遇到错误就停止。

对于每组数据，你的输出与标准结果匹配，则认为该组数据通过，否则，认为该组数据不通过。

将根据你通过组数的占所有测试数据组数的比重计算你的得分。

如果你使用的是 Java，你可以使用 Java 的 Matrix 包来简化你的矩阵运算，例如：

• 你可以用 inverse() 来求矩阵的逆
• 你可以用 eigenValueDecompostion() 来求矩阵的特征值

如果你使用的是 Python， 你可以使用 numpy 包来简化你的矩阵运算，例如：

• 你可以用 cov() 来代替 $\displaystyle C=\frac{1}{m-1}{X^T}{X}$ 求协方差矩阵
• 你可以用 linalg.eig() 求矩阵的特征值和特征向量
• 你可以用 argsort() 来排序

Special Judge

如上文所言，不同学生降维后的正负号可能是不一样的，因此，我的判题采用了绝对值的方法，先对所有的数取绝对值，然后比较在$10^{-4}$精度下是否相等。

if (fabs(od - ad) > 1E-4)
    score = 0;

Cases

在Iris.data.txt文件中，我去除了最后一个标签字段。

之后，对于 $150$ 条记录、每条记录 $4$ 个字段，我分别要求输出了降维到 $1$ 维、$2$ 维和 $3$ 维的矩阵。

另外，我随机生成了 $2$ 组较小规模的数据，作为样例公开，以便同学调试。

最后，我增加了abalone数据集，对大规模、高维度（$8$ 维）数据的主成分分析降维进行测评。

Sandbox

因为判题系统是在沙箱环境中，所以很多功能是被限制使用的，例如fork()就是无法使用的。

因此，虽然 Python(SCI) 安装了包括SciKit-Learn、NLTK等库，但是事实上并没有办法正常调用SciKit-Learn。

当然，我没有做深入的测试，也许，通过设置与matplotlib类似的方法（matplotlib.use("Agg")）可以正常调用也说不定？

Generate Pictures

助教最开始的做法是要求生成图片，说实话我是懒得搞这些东西的。

虽然我很多时候确实喜欢有图形化界面的东西，不喜欢命令行，所以像问题求解的 Percolation 和 Seam-Carving 作业，我都是做了一个 GUI 程序作为我的作业，而不是简单的 C/C++ Console 程序。

但是我明明数据已经计算出来了，还偏要我去给你搞一张图，我是懒得搞的，尤其是遇到 Python，要知道我非常非常非常反感 Python。

而且，因为每位同学选择降低的维度不同，生成的图片也不同，所以光看图片也没有什么检验的价值，最终还是要人工看代码（谁知道你的图片是不是直接SciKit-Learn加matplotlib调用的呢），因此为了尽量减少人工的负担，把测评工作交给了 OJ，这回就变成了一题实实在在的需要提交完整代码的题了。