
下载完整文章:
Thanks to 10175102128 for his pointing out a potential bug in his submit #1293284.
/** * 检查交换给定的两个皇后会不会减少冲突数 * @param i 第i行 * @param j 第j行 * @return 交换后的冲突数的变化量,小于0表示冲突减少 */ int swapWillReduceCollisions(int i, int j) { // This function is ill-implemented // Bugs: swapWillReduceCollisions(i, i) => 8, i = 1, 2, ... // UTD: When A and B are located in the same diagonal, whether major or minor // the computation may fall into errors.
问题介绍
介绍需要求解的问题
八皇后问题是一个以国际象棋为背景的问题:
如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?
该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:
在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击
即任意两个皇后都不能处于同一行、同一列或同一斜线上
问有多少种摆法
下面把这个问题抽象成$n$皇后问题
例如,当$n=4$的时候,就是四皇后问题
问题变成:在一个$4\times4$的国际象棋棋盘上,一次一个地摆布$4$枚皇后棋子,摆好后要满足每行、每列和正反对角线上只允许出现一枚棋子,即棋子之间不许相互俘获,要求给出一种合法的摆放方式
例如下面给出一个合法的摆放方式
| Q | |||
|---|---|---|---|
| Q | |||
| Q | |||
| Q |
而下面这种摆放是不合法的
| Q | |||
|---|---|---|---|
| Q | |||
| Q | |||
| Q |
现在把棋盘扩大到$n\times n$的规模,其他规则不变
输入:皇后的数目,例4
输出:任意一种合法的摆放方式,即第1行至第N行皇后对应的列号,例(2, 4, 1, 3)
约定:下标从0开始,即第0行到第n-1行
输出格式:(行号,列号)
为什么要采用我们介绍的方法求解
皇后问题从来都是算法设计的经典问题
诞生了不计其数的解法
其中比较经典的算法是回溯法、深度优先搜索和广都优先搜索
回溯策略属于盲目搜索的一种,最直接的实现方法是递归法
图搜索策略是实现从一个隐含图中,生成出一部分确实含有一个目标结点的显式表示子图的搜索过程
深度优先搜索和广度优先搜索这两种算法在数据结构中都分别使用堆栈和队列来实现过
在这里,重新运用一般图搜索的框架来重新实现深度优先搜索和广度优先搜索
但是绝大多数的算法,包括以上述三种算法为代表的算法,都只能求解规模较小的n
而对于数百万的规模的n来说,需要花费若干分钟甚至若干小时,都不一定能完成任务
所以,为了解决百万皇后,需要用到随机算法、启发式搜索
程序设计与算法分析
回溯法
数据结构定义
回溯法主要用到递归
Q是一个二维数组
某行某列的值为1说明这里放了皇后
否则就是值为0
算法描述
先处理第1个皇后
在当前列加1的位置开始搜索
不满足条件的话继续搜索下一列位置
若存在满足条件的列且是最后一个皇后,则得到一个最终解,输出
否则,处理下一个皇后
若不存在满足条件的列,则回溯
第k个皇后复位为0,回溯到前一个皇后
算法简介
回溯法的基本思想是按照深度优先搜索的策略
从根节点开始搜索
当到某个节点时要判断是否是包含问题的解
如果包含就从该节点继续搜索下去
如果不包含,就向父节点回溯
深度优先搜索
数据结构定义
以下这些定义与一般图搜索框架的定义一致
• 结点深度
• 路径
• 路径耗散值
• 扩展一个结点
下面解释一些数据结构的定义
• OPEN表:用于存放刚生成的节点
• CLOSED表:用于存放将要扩展或已扩展的节点
• G:显式表示的搜索图
• Search:封装好的类
• target:目标
• start :主方法,调用即可求解,如果找到结果返回true,否则返回false
• Node:表示结点 extends Point:二元点对,表示横纵坐标
• parent:指向父节点
一般图搜索的框架
class Search {
int target;
public Search(int target) {
this.target = target;
}
LinkedList<Node> open = new LinkedList<Node>();
LinkedList<Node> closed = new LinkedList<Node>();
SearchingGraphic graphic;
Node latest;
public boolean start(Node source) {
// graphic表示搜索图,source为初始节点,设置OPEN表,最初只含初始节点
graphic = new SearchingGraphic(source);
open.add(source);
while (true) {
// 无解
if (open.isEmpty()) {
return false;
}
Node currentNode = open.pollFirst();
closed.add(currentNode);
// 由最后一个节点层层返回父节点可以给出解路径
if (isTarget(currentNode)) {
latest = currentNode;
return true;
}
// 扩展子节点
ArrayList<Node> m = expand(currentNode);
if (m.isEmpty()) {
// TODO m为空,根据具体题目不同可能有不同的处理
} else {
// m非空,加入到图G,然后设置父节点
graphic.add(m);
setPointer(m, currentNode);
}
open.sort(new Comparator<Node>(){
@Override
public int compare(Node o1, Node o2) {
// TODO 按照某种原则排序,该原则根据具体题目不同可能有不同的处理
return 0;
}
});
}
}
private void setPointer(ArrayList<Node> m, Node parent) {
for (Node n : m) {
if (open.contains(n)) {
//TODO 如果节点在OPEN表中,根据具体题目不同可能有不同的处理
} else if (closed.contains(n)) {
//TODO 如果节点在CLOSED表中,根据具体题目不同可能有不同的处理
} else {
// 加入到OPEN表,设置父节点
open.add(n);
n.setParent(parent);
}
}
}
private ArrayList<Node> expand(Node node) {
ArrayList<Node> m = new ArrayList<Node>();
// TODO 实现扩展,具体题目不同可能有不同的处理
return m;
}
private boolean isTarget(Node node) {
// TODO 判断是不是目标,具体题目不同可能有不同的处理
return false;
}
}
算法描述
• 如何确定OPEN表是按照什么原则排序的
所谓深度优先搜索,就是在每次扩展一个结点时,选择到目前为止深度最深的结点优先扩展
由于子结点的深度要大于父结点的深度,实际上OPEN表是按照结点的深度进行排序的,深度深的结点排在前面,深度浅的结点排在后面
分析深度优先搜索,可以知道,将m加入到Open表中,应该就加在Open表的最前面,那么这样可以保证深度大的结点可以优先得到扩展
那么,只要把不在Open表或者不在Closed表中的结点,加入到队列(链表)的开头,就可以了,后面不需要再次排序
于是,只要open.addLast(m);就可以了,不用再做 open.sort(new Comparator<Node>(){...})
• 如何判断某个结点是不是在表中
判断依据是三元组,即(横坐标,纵坐标,父亲节点)
如果只有横纵坐标一致但父亲节点不一样,应该认为是不同的结点
• 如何判断目标点
已经存在某个点的行数等于皇后数的时候就可以直接判断得到结果了
• 如何得到最终的棋盘摆放
只要从最后一个结点,逐层往上一直找到起点就可以了
逐层往上就是通过父节点来完成的
• 如何判断这是一个起点
一种方法是有且仅有起点的父节点是null
那么只要当结点node不是null的时候,就算是合法的摆放,然后node=node.parent
另一种方法是有且仅有起始节点的父节点是自己
同样可以逐层找到所有的摆放
所以,其实不需要使用Stack或者Queue来存储搜索的路径
尽管一般情况下我们常用Stack来深搜,用Queue来广搜
但是一般图搜索框架使得程序只需要把每次搜索的搜索结点存到搜索图中
由于node的主要成员变量是横纵坐标和父节点,所以可以做到不重不漏
伪代码描述
INITIAL: G.add(source) open.add(source) closed为空 LOOP: (OPEN为空)⇒(没有结果) n=open.first() (n是目标)⇒(找到结果) open.removeFirst() closed.add(n) 扩展n得到若干个m 把m加到图G 把不在OPEN或CLOSED表中的m加到OPEN表最前面,使深度大的结点可以优先扩展 标记这些m的父节点为n GO→LOOP
流程图
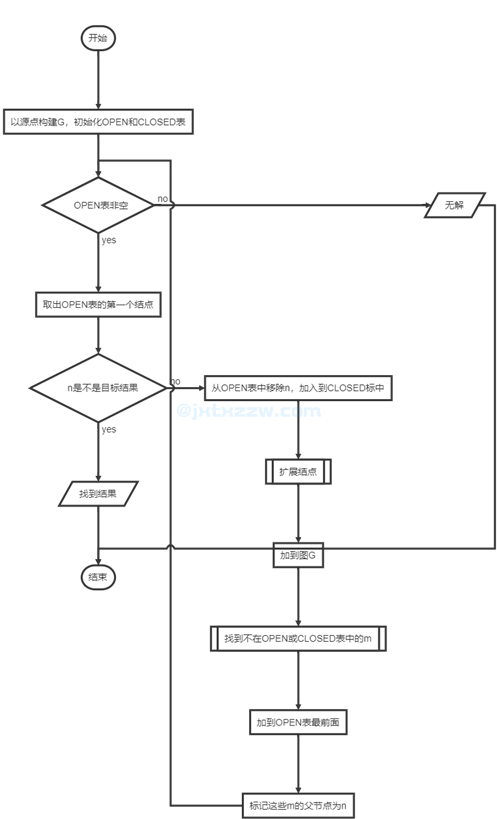
广度优先搜索
数据结构定义
与深度优先算法中用到的数据结构完全一样
算法描述
与深度优先算法中用到的算法基本一样
唯一的区别是,OPEN表的排序标准不同,把不在Open表或者不在Closed表中的结点,加入到队列(链表)的末尾
算法框图
与深度优先算法中用到的算法框图基本一样
百万皇后
数据结构定义
300万皇后问题的算法
参考了Rok sosic和Jun Gu的Polynomial Time Algorithms for the N-Queen Problem中的QS算法
百万皇后的主要思想
随机地生成一张摆放
取出可以相互攻击的皇后,然后任意取出一个皇后,看看他们交换是不是可以减少冲突
如果可以,交换,否则,不交换
数据存放的形式
第i行的皇后放在第queen[i]列
i遍历0~n-1,保证了每一行只有1个皇后,所以不会存在行的冲突
queen[i]列是一个[0..n-1]的序列
如果保证这个序列不重不漏,那么每一列也就只有1个皇后,所以不会存在列的冲突
另外,如果保证在每次交换的过程中,第i行的皇后和第j行的皇后交换,指的是他们的列交换,所以行和列都还是不重不漏的[0..n-1]的序列
于是只要每次维护正反对角线是不是有冲突就可以了
变量声明
rand()范围太小,要超大规模随机数,所以要这个,注意这个是unsigned long long int,所以要强制类型转换成int
typedef std::subtract_with_carry_engine<std::uint_fast64_t, 48, 5, 12> ranlux48_base;
//n表示皇后数量
int n;
//queen[i]表示第i行的皇后在第几列
int queen[MAXN];
//表示哪些皇后是可以相互攻击的
attack[MAXN];
//正反对角线的冲突数量
int diagonalNegative[2 * MAXN + 7];
int diagonalPositive[2 * MAXN + 7];
//总冲突数
int collisions;
//记录某一列是不是已经放了东西了,这保证[0..n-1]序列不重不漏,所以列一定不会有冲突
bool columnUsed[MAXN] = {false};
函数声明
/** * 想在第row行第col列放皇后,检查这个皇后是不是和以前放的有冲突 * @param row 行数 * @param col 列数 * @return 如果没有冲突,返回true,否则,false */ bool check(int row, int col) /** * 随机生成一个棋盘布局 */ void generateARadomPermutation() /** * 执行交换给定两行的皇后 * @param i 第i行 * @param j 第j行 */ void performSwap(int i, int j) /** * 检查交换给定的两个皇后会不会减少冲突数 * @param i 第i行 * @param j 第j行 * @return 交换后的冲突数的变化量,小于0表示冲突减少 */ int swapWillReduceCollisions(int i, int j) /** * 计算冲突 * @return 冲突数量 */ int computeCollisions() /** * 获得能够相互攻击的皇后的编号 * @return 能够相互攻击的皇后的个数 */ int computeAttacks()
算法描述
随机地生成一张摆放
取出可以相互攻击的皇后,然后任意取出一个皇后,看看他们交换是不是可以减少冲突
如果可以,交换,否则,不交换
优化细节
- 前THRESHOLD行要保证没有冲突,这是为了减少collision的数量,尽可能加速程序运行,这里的THRESHOLD参考了几篇论文,最终定在$\frac{5}{12}$,放下去之前要check
- check不能每次遍历比较,直接看对角线数组是不是为0
- 检查交换给定的两个皇后会不会减少冲突数,计算的结果用delta表示变化量,一方面可以用delta的正负来表示是不是交换了更好,另一个是可以在更新collision的时候直接加上delta就好了
- 容斥原理,如果正好是同一条对角线,要去掉重复计算的那个
- 冲突数按照$C_n^2$计算,而不是有x个皇后计算x-1个冲突,那样的话每次冲突减少的都是没几个,一个两个,三个五个
- 能够相互攻击的皇后数量不等于冲突数量
- n要求为正整数,n=2和n=3无解,所以直接判断掉了
- 计算一个阈值,当冲突小于阈值的时候重新计算attack数组,这里的常系数定义参考了Rok sosic和Jun Gu的QS2算法的定义,$C_1$取0.53
- 最大化N较小的时候的运行速度,对较大的N没有影响,这里的常系数定义参考了Rok sosic和Jun Gu的QS2算法的定义,$C_2$取32
流程图
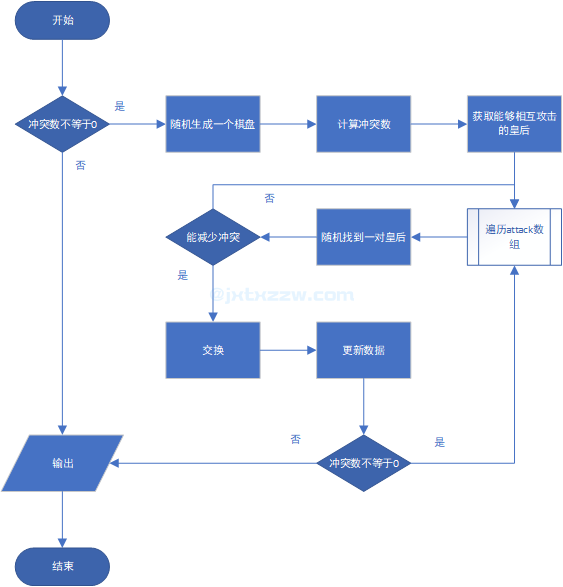
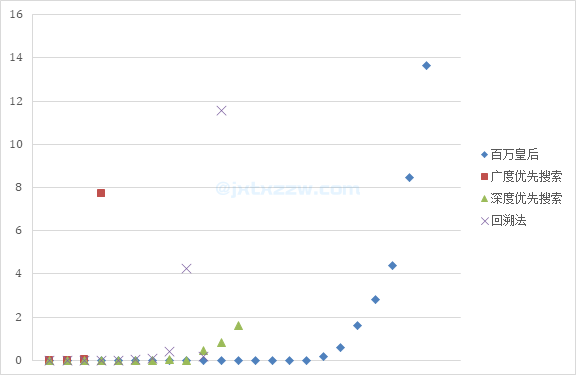
实验结果
| N | 回溯法 | 深度优先搜索 | 广度优先搜索 | 百万皇后 (随机算法) |
|---|---|---|---|---|
| 4 | 0.000 | 0.001 | 0.002 | 0.000 |
| 8 | 0.001 | 0.003 | 0.003 | 0.000 |
| 10 | 0.002 | 0.003 | 0.022 | 0.000 |
| 12 | 0.002 | 0.003 | 7.728 | 0.000 |
| 14 | 0.003 | 0.008 | 不适用 | 0.000 |
| 16 | 0.016 | 0.008 | 不适用 | 0.000 |
| 18 | 0.074 | 0.012 | 不适用 | 0.000 |
| 20 | 0.404 | 0.019 | 不适用 | 0.000 |
| 22 | 4.248 | 0.014 | 不适用 | 0.000 |
| 25 | 0.158 | 0.441 | 不适用 | 0.000 |
| 28 | 11.574 | 0.847 | 不适用 | 0.000 |
| 30 | 不适用 | 1.597 | 不适用 | 0.000 |
| 50 | 不适用 | 不适用 | 不适用 | 0.000 |
| 100 | 不适用 | 不适用 | 不适用 | 0.001 |
| 1000 | 不适用 | 不适用 | 不适用 | 0.001 |
| 10000 | 不适用 | 不适用 | 不适用 | 0.014 |
| 100000 | 不适用 | 不适用 | 不适用 | 0.161 |
| 250000 | 不适用 | 不适用 | 不适用 | 0.602 |
| 500000 | 不适用 | 不适用 | 不适用 | 1.610 |
| 750000 | 不适用 | 不适用 | 不适用 | 2.798 |
| 1000000 | 不适用 | 不适用 | 不适用 | 4.392 |
| 2000000 | 不适用 | 不适用 | 不适用 | 8.452 |
| 3000000 | 不适用 | 不适用 | 不适用 | 13.625 |
程序源代码
回溯法
#include <stdio.h>
#define MAXN 50
#define QUEEN 1
int n = 0;
int Q[MAXN][MAXN] = {{0}};
int solved = false;
int isValid(int row, int col) {
for (int j = 0; j < n; j++)
if (Q[row][j] == QUEEN && col != j)
return false;
for (int i = 0; i < n; i++)
if (Q[i][col] == 1 && row != i)
return false;
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--)
if (Q[i][j] == QUEEN)
return false;
for (int i = row + 1, j = col + 1; i < n && j < n; i++, j++)
if (Q[i][j] == QUEEN)
return false;
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++)
if (Q[i][j] == QUEEN)
return false;
for (int i = row + 1, j = col - 1; i < n && j >= 0; i++, j--)
if (Q[i][j] == QUEEN)
return false;
return true;
}
void Queen(int row) {
if (row == n) {
for (int row = 0; row < n; row++)
for (int col = 0; col < n; col++)
if (Q[row][col] == QUEEN)
printf("(%d, %d) ", row, col);
printf("\n");
solved = true;
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col)) {
Q[row][col] = QUEEN;
Queen(row + 1);
if (solved) return;
Q[row][col] = !QUEEN;
}
}
}
int main() {
scanf("%d", &n);
Queen(0);
return 0;
}
深度优先搜索
import java.awt.Point;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
in.close();
for (int i = 0; i < n; ++i) {
Search source = new Search(n);
if (source.start(new Node(0, i)) == true) {
LinkedList<Node> result = source.getResult();
for (Node node : result) {
System.out.println(node);
}
System.exit(0);
}
}
}
}
class Search {
int target;
public Search(int target) {
this.target = target;
}
LinkedList<Node> open = new LinkedList<Node>();
LinkedList<Node> closed = new LinkedList<Node>();
SearchingGraphic graphic;
Node latest;
public boolean start(Node source) {
graphic = new SearchingGraphic(source);
open.add(source);
while (true) {
if (open.isEmpty()) {
return false;
}
Node currentNode = open.pollFirst();
closed.add(currentNode);
if (isTarget(currentNode)) {
latest = currentNode;
return true;
}
ArrayList<Node> m = expand(currentNode);
if (m.isEmpty()) {
} else {
graphic.add(m);
setPointer(m, currentNode);
}
}
}
private void setPointer(ArrayList<Node> m, Node parent) {
for (Node n : m) {
if (!open.contains(n) || !closed.contains(n)) {
open.addFirst(n);
n.setParent(parent);
}
}
}
private ArrayList<Node> expand(Node node) {
ArrayList<Node> m = new ArrayList<Node>();
int row = node.x + 1;
for (int col = 0; col < target; col++) {
Node n = new Node(row, col);
if (isValid(n, node)) {
m.add(n);
}
}
return m;
}
private boolean isValid(Node n, Node node) {
while (node != null) {
if (n.y == node.y)
return false;
if (Math.abs(n.y - node.y) == Math.abs(n.x - node.x))
return false;
node = node.getParent();
}
return true;
}
private boolean isTarget(Node node) {
return node.x == target - 1;
}
public LinkedList<Node> getResult() {
LinkedList<Node> result = new LinkedList<Node>();
Node node = latest;
while (node != null) {
result.addFirst(node);
node = node.getParent();
}
return result;
}
}
class SearchingGraphic {
ArrayList<Node> datalist = new ArrayList<Node>();
public SearchingGraphic(Node source) {
datalist.add(source);
}
public void add(ArrayList<Node> m) {
for (Node p : m) {
datalist.add(p);
}
}
}
class Node extends Point implements Comparable<Node> {
private static final long serialVersionUID = 1L;
private Node parent;
public Node getParent() {
return parent;
}
public void setParent(Node parent) {
this.parent = parent;
}
public Node(int x, int y) {
super(x, y);
parent = null;
}
@Override
public int compareTo(Node o) {
// TODO
return 0;
}
}
广度优先搜索
import java.awt.Point;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
in.close();
for (int i = 0; i < n; ++i) {
Search s = new Search(n);
if (s.start(new Node(0, i)) == true) {
LinkedList<Node> result = s.getResult();
for (Node node : result) {
System.out.println(node);
}
System.exit(0);
}
}
}
}
class Search {
int target;
public Search(int target) {
this.target = target;
}
LinkedList<Node> open = new LinkedList<Node>();
LinkedList<Node> closed = new LinkedList<Node>();
SearchingGraphic graphic;
Node latest;
public boolean start(Node source) {
graphic = new SearchingGraphic(source);
open.add(source);
while (true) {
if (open.isEmpty()) {
return false;
}
Node currentNode = open.pollFirst();
// System.out.println(currentNode);
closed.add(currentNode);
if (isTarget(currentNode)) {
latest = currentNode;
return true;
}
ArrayList<Node> m = expand(currentNode);
if (m.isEmpty()) {
} else {
graphic.add(m);
setPointer(m, currentNode);
}
}
}
private void setPointer(ArrayList<Node> m, Node parent) {
for (Node n : m) {
if (!open.contains(n) || !closed.contains(n)) {
Node newN = new Node(n.x, n.y);
newN.setParent(parent);
open.addLast(newN);
}
}
}
private ArrayList<Node> expand(Node node) {
ArrayList<Node> m = new ArrayList<Node>();
int row = node.x + 1;
for (int col = 0; col < target; col++) {
Node n = new Node(row, col);
if (isValid(n, node)) {
m.add(n);
}
}
return m;
}
private boolean isValid(Node n, Node node) {
while (node != null) {
if (n.y == node.y)
return false;
if (Math.abs(n.y - node.y) == Math.abs(n.x - node.x))
return false;
node = node.getParent();
}
return true;
}
private boolean isTarget(Node node) {
return node.x == target - 1;
}
public LinkedList<Node> getResult() {
LinkedList<Node> result = new LinkedList<Node>();
Node node = latest;
while (node != null) {
result.addFirst(node);
node = node.getParent();
}
return result;
}
}
class SearchingGraphic {
ArrayList<Node> datalist = new ArrayList<Node>();
public SearchingGraphic(Node source) {
datalist.add(source);
}
public void add(ArrayList<Node> m) {
for (Node p : m) {
datalist.add(p);
}
}
}
class Node extends Point implements Comparable<Node> {
private static final long serialVersionUID = 1L;
private Node parent;
// private int sortingBasis;
public Node getParent() {
return parent;
}
public void setParent(Node parent) {
this.parent = parent;
}
public Node(int x, int y) {
this.x = x;
this.y = y;
parent = null;
}
@Override
public int compareTo(Node o) {
// TODO
return 0;
}
@Override
public boolean equals(Object o) {
Node n = (Node) o;
if (parent == null) {
if (n.parent == null) {
return n.x == x && n.y == y;
} else {
return false;
}
} else {
if (n.parent == null) {
return false;
} else {
return n.x == x && n.y == y;
}
}
}
}
百万皇后
#include <bits/stdc++.h>
#define MAXN 5000007
using namespace std;
// rand()范围太小,要超大规模随机数,所以要这个,注意这个是unsigned long long int,所以要强制类型转换成int
typedef std::subtract_with_carry_engine<std::uint_fast64_t, 48, 5, 12> ranlux48_base;
// n表示皇后数量
int n;
// queen[i]表示第i行的皇后在第几列
int queen[MAXN];
// 表示哪些皇后是可以相互攻击的
int attack[MAXN];
// 正反对角线的冲突数量
int diagonalNegative[2 * MAXN + 7];
int diagonalPositive[2 * MAXN + 7];
// 总冲突数
int collisions;
// 记录某一列是不是已经放了东西了,这保证[0..n-1]序列不重不漏,所以列一定不会有冲突
bool columnUsed[MAXN] = {false};
/**
* 想在第row行第col列放皇后,检查这个皇后是不是和以前放的有冲突
* @param row 行数
* @param col 列数
* @return 如果没有冲突,返回true,否则,false
*/
bool check(int row, int col) {
int negativeIndex = row + col;
int positiveIndex = row - col;
return (diagonalNegative[negativeIndex] == 0 && diagonalPositive[n - 1 + positiveIndex] == 0);
}
/**
* 随机生成一个棋盘布局
*/
void generateARadomPermutation() {
ranlux48_base rb;
// 前THRESHOLD行要保证没有冲突,这是为了减少collision的数量,尽可能加速程序运行,这里的THRESHOLD参考了几篇论文,最终定在5/12
const int THRESHOLD = (int) (5.0 / 12.0 * n);
int generatedQueenNumber = 0;
memset(diagonalPositive, 0, 2 * n * sizeof(int));
memset(diagonalNegative, 0, 2 * n * sizeof(int));
while (generatedQueenNumber < n) {
int col;
do {
col = (int) (rb() % n);
} while (columnUsed[col]);
// 前面5/12行是没有冲突的,所以放下去之前要check
if (generatedQueenNumber < THRESHOLD)
if (check(generatedQueenNumber, col) == false) { continue; }
queen[generatedQueenNumber] = col;
columnUsed[col] = true;
int negativeIndex = generatedQueenNumber + col;
++diagonalNegative[negativeIndex];
int positiveIndex = generatedQueenNumber - col;
++diagonalPositive[n - 1 + positiveIndex];
++generatedQueenNumber;
}
}
/**
* 执行交换给定两行的皇后
* @param i 第i行
* @param j 第j行
*/
void performSwap(int i, int j) {
// 首先更新对角线的冲突数组,减去原来的冲突数
--diagonalNegative[i + queen[i]];
--diagonalNegative[j + queen[j]];
--diagonalPositive[n - 1 + i - queen[i]];
--diagonalPositive[n - 1 + j - queen[j]];
// 交换皇后
int tmp = queen[i];
queen[i] = queen[j];
queen[j] = tmp;
// 把交换后增加的冲突加入到对角线冲突数组
++diagonalNegative[i + queen[i]];
++diagonalNegative[j + queen[j]];
++diagonalPositive[n - 1 + i - queen[i]];
++diagonalPositive[n - 1 + j - queen[j]];
}
/**
* 检查交换给定的两个皇后会不会减少冲突数
* @param i 第i行
* @param j 第j行
* @return 交换后的冲突数的变化量,小于0表示冲突减少
*/
int swapWillReduceCollisions(int i, int j) {
int delta = 0;
// 计算原来正反对角线的冲突量,交换后会使得这些冲突减少
delta -= diagonalNegative[i + queen[i]] - 1;
delta -= diagonalNegative[j + queen[j]] - 1;
// 容斥原理,如果正好是同一条对角线,要去掉重复计算的那个
if (i + queen[i] == j + queen[j]) {
++delta;
}
delta -= diagonalPositive[n - 1 + i - queen[i]] - 1;
delta -= diagonalPositive[n - 1 + j - queen[j]] - 1;
if (i - queen[i] == j - queen[j]) {
++delta;
}
//计算新对角线的冲突量,交换后的新位置将会额外增加这些冲突
delta += diagonalNegative[i + queen[j]];
delta += diagonalNegative[j + queen[i]];
if (i + queen[j] == j + queen[i]) {
++delta;
}
delta += diagonalPositive[n - 1 + i - queen[j]];
delta += diagonalPositive[n - 1 + j - queen[i]];
if (i - queen[j] == j - queen[i]) {
++delta;
}
return delta;
}
/**
* 计算冲突
* @return 冲突数量
*/
int computeCollisions() {
int collisions = 0;
// 遍历对角线数组计算冲突数量
for (int i = 0; i < 2 * n - 1; ++i) {
collisions += diagonalNegative[i] * (diagonalNegative[i] - 1) / 2;
collisions += diagonalPositive[i] * (diagonalPositive[i] - 1) / 2;
}
return collisions;
}
/**
* 获得能够相互攻击的皇后的编号
* @return 能够相互攻击的皇后的个数
*/
int computeAttacks() {
/*
* 注:能够相互攻击的皇后数量不等于冲突数量
*/
memset(attack, 0, n * sizeof(int));
int numberOfAttacks = 0;
for (int i = 0; i < n; ++i) {
int negativeIndex = i + queen[i];
int positiveIndex = i - queen[i];
// 如果某皇后所在对角线有其他皇后,那就是可以攻击的,计数器加1,并记录这是第几个皇后
if (diagonalNegative[negativeIndex] > 1 || diagonalPositive[n - 1 + positiveIndex] > 1) {
attack[numberOfAttacks] = i;
++numberOfAttacks;
}
}
return numberOfAttacks;
}
int main() {
ranlux48_base rb;
cin >> n;
if (n <= 0 || n == 2 || n == 3) {
// n要求为正整数,n=2和n=3无解,所以直接判断掉了
cout << "No solution." << endl;
} else {
int beginTime = clock();
// C1是为了计算一个阈值,当冲突小于阈值的时候重新计算attack数组,这里的常系数定义参考了Rok sosic和Jun Gu的QS2算法的定义,C1取0.53
const double C1 = 0.45;
// C2是为了最大化N较小的时候的运行速度,对较大的N没有影响,这里的常系数定义参考了Rok sosic和Jun Gu的QS2算法的定义,C2取32
const double C2 = 32;
do {
generateARadomPermutation();
collisions = computeCollisions();
int limit = (int) (C1 * collisions);
int numberOfAttacks = computeAttacks();
int loopCount = 0;
do {
if (collisions == 0) {
break;
}
// 只遍历能够相互攻击的皇后
for (int k = 0; k < numberOfAttacks; ++k) {
// 找到一个具有攻击性的皇后,再随机地找一个和自己不一样的皇后
int i = attack[k];
int j;
do {
j = (int) (rb() % n);
} while (i == j);
int delta;
// 如果交换后的冲突是减小的,执行交换
if ((delta = swapWillReduceCollisions(i, j)) < 0) {
// 更新冲突数,并执行交换
collisions += delta;
performSwap(i, j);
// 冲突数为0,找到解,输出,冲突数小于阈值,重新计算阈值和attack数组
if (collisions == 0) {
break;
}
if (collisions < limit) {
limit = (int) (C1 * collisions);
numberOfAttacks = computeAttacks();
}
}
}
loopCount += numberOfAttacks;
} while (loopCount <= C2 * n);
} while (collisions != 0);
int endTime = clock();
// 输出
// for (int i = 0; i < n; ++i) printf("(%d, %d)\n", i, queen[i]);
// 输出耗费的时间
printf("Time cost: %f second(s).\n", (double) (endTime - beginTime) / CLOCKS_PER_SEC);
}
return 0;
}
关于百万皇后问题中打超大规模随机数,你可以查看:

yuanlaihaiyouzishuyaoqiu
t’q’l
tql
modalao
tql
tql
tql