计蒜客上的一道深搜题。

从深搜的角度说，没有什么花样，就是数独，DFS，判断是不是用过了这个数字，然后放满所有的格子以后计算得分，取最大得分。

这道题我觉得他很好，是因为有很多剪枝的地方，稍不注意就会超时。

原题如下：

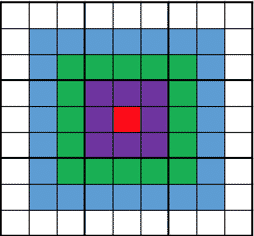
蒜头君天资聪颖，酷爱数学，尤其擅长做数独游戏。不过普通的数独游戏已经满足不了蒜头君了，于是他发明了一种“金字塔数独”：下图即为金字塔数独。和普通数独一样，在 9×9 的大九宫格中有 9 个 3×3 的小九宫格（用粗黑色线隔开的）。要求每个格子上都有一个 1 到 9 的数字，每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。但金字塔数独的每一个格子都有一个分值，类似金字塔的俯视图。如图所示，白色格子为 6 分，蓝色格子为 7 分，绿色格子为 8 分，紫色格子为 9 分，红色格子为 10 分。颜色相同的格子分值一样，离中心越近则分值越高。

金字塔数独的总分等于每个格子上的数字和对应的分值乘积之和。现在蒜头君给定金字塔数独的若干数字，请问如何填写，可以使得金字塔数独的总分最高。

输入格式：输入一共 9 行。每行输入 9 个整数（每个数都在 0—9 的范围内），每两个整数之间用一个空格隔开，“0”表示该格子为空。

输出格式：输出为一行，输出一个整数，代表金字塔数独的最高总分。如果数独无解，则输出 −1。

#include <stdio.h>
#include <iostream>

#define WIDTH 3
#define BOARD_SIZE 9
#define CANDIDATES_RANGE 9

const int SCORE_WEIGHT[BOARD_SIZE][BOARD_SIZE] = {
        {6, 6, 6, 6, 6,  6, 6, 6, 6},
        {6, 7, 7, 7, 7,  7, 7, 7, 6},
        {6, 7, 8, 8, 8,  8, 8, 7, 6},
        {6, 7, 8, 9, 9,  9, 8, 7, 6},
        {6, 7, 8, 9, 10, 9, 8, 7, 6},
        {6, 7, 8, 9, 9,  9, 8, 7, 6},
        {6, 7, 8, 8, 8,  8, 8, 7, 6},
        {6, 7, 7, 7, 7,  7, 7, 7, 6},
        {6, 6, 6, 6, 6,  6, 6, 6, 6}
};

int board[BOARD_SIZE][BOARD_SIZE] = {{0}};

int ans = -1;

// 暴力搜索会超时 case 5，改成标记
//int isValid(int row, int col, int val) {
//    for (int i = 0; i < BOARD_SIZE; i++)
//        if (i != row && board[i][col] == val)
//            return false;
//    for (int j = 0; j < BOARD_SIZE; j++)
//        if (j != col && board[row][j] == val)
//            return false;
//    int majorRow = row / WIDTH;
//    int majorCol = col / WIDTH;
//    for (int i = majorRow * WIDTH; i < majorRow * WIDTH + WIDTH; i++)
//        for (int j = majorCol * WIDTH; j < majorCol * WIDTH + WIDTH; j++)
//            if (i != row && j != col && board[i][j] == val)
//                return false;
//    return true;
//}

// 以 rowUsed 为例，rowUsed[i][j] == true 表示第 i 行的数字 j 已经出现过
bool rowUsed[BOARD_SIZE][CANDIDATES_RANGE + 1] = {{0}};
bool colUsed[BOARD_SIZE][CANDIDATES_RANGE + 1] = {{0}};
bool gridUsed[BOARD_SIZE][CANDIDATES_RANGE + 1] = {{0}};

bool isValid(int row, int col, int val) {
    return (!rowUsed[row][val] && !colUsed[col][val] && !gridUsed[row / WIDTH * WIDTH + col / WIDTH][val]);
}

void setNumber(int row, int col, int val, bool status) {
    board[row][col] = status ? val : 0;
    colUsed[col][val] = status;
    rowUsed[row][val] = status;
    gridUsed[row / WIDTH * WIDTH + col / WIDTH][val] = status;
}


int calculateScore() {
    int score = 0;
    for (int i = 0; i < BOARD_SIZE; i++)
        for (int j = 0; j < BOARD_SIZE; j++)
            score += board[i][j] * SCORE_WEIGHT[i][j];
    return score;
}

void dfs(int depth, int candidatesNumber) {
    if (depth == candidatesNumber) {
        ans = std::max(calculateScore(), ans);
        return;
    }

    /*
     * 这里有个 trick，可能要看了题解（数据）才知道了
     * i 从 0 到 9，j 从 0 到 9，case 3 和 case 4 会超时，从 9 反过来回到 0 就不会
     * 本质上没有区别，只是数据恶心了些
     */
    for (int i = BOARD_SIZE - 1; i >= 0; i--)
        for (int j = BOARD_SIZE - 1; j >= 0; j--) {
            if (board[i][j] != 0)
                continue;
            for (int candidate = 1; candidate <= CANDIDATES_RANGE; candidate++) {
                if (isValid(i, j, candidate)) {
                    setNumber(i, j, candidate, true);
                    dfs(depth + 1, candidatesNumber);
                    setNumber(i, j, candidate, false);
                }
            }
            return; // 这个 return 必须要剪枝，9个数都放完了就 return，否则会很慢很慢很慢，样例都过不了
        }

}

int main() {
    int candidatesNumber = 0;
    for (int i = 0; i < BOARD_SIZE; i++)
        for (int j = 0; j < BOARD_SIZE; j++) {
            int x;
            scanf("%d", &x);
            setNumber(i, j, x, true);
            if (x == 0)
                candidatesNumber++;
        }
    dfs(0, candidatesNumber);
    printf("%d", ans);
    return 0;
}