
这是普林斯顿大学算法课的第 8 次作业,利用网络流(最大流、最小切)来判断哪些球队在接下来的比赛中已经不可能获得冠军、提前出局。
从题目给定的样例,我们可以发现确定谁被消除并不是一件容易的事情。
w[i] l[i] r[i] g[i][j] i team wins loss left Atl Phi NY Mon ------------------------------------------------ 0 Atlanta 83 71 8 - 1 6 1 1 Philadelphia 80 79 3 1 - 0 2 2 New York 78 78 6 6 0 - 0 3 Montreal 77 82 3 1 2 0 -
Montreal 在数学上已经被淘汰,因为它只剩下 3 场比赛,因此最多可以赢得 80 场胜利,而亚特兰大已经有 83 场胜利,它已经不可能是冠军。
而 Philadelphia 也被淘汰。这个理由并不像上面那个理由这么显而易见:它可以最多获得 83 场生日,这似乎足以与 Atlanta 并列。但,这将要求 Atlanta 输掉所有剩余的比赛,包括对 New York 的 6 场比赛,然而,在这种情况下,New York 将以 84 场胜利结束,最终赢得冠军。因此,尽管 New York 的获胜次数少于 Philadelphia,但在数学上尚未被淘汰。
w[i] l[i] r[i] g[i][j] i team wins loss left NY Bal Bos Tor Det --------------------------------------------------- 0 New York 75 59 28 - 3 8 7 3 1 Baltimore 71 63 28 3 - 2 7 7 2 Boston 69 66 27 8 2 - 0 3 3 Toronto 63 72 27 7 7 0 - 3 4 Detroit 49 86 27 3 7 3 3 -
在这个例子中,Detroit 获胜的几率显然是渺茫的,在所有队伍都只剩下 27、28 场比赛没有完成的情况下,获胜不足 50 场的 Detroit 很难角逐冠军。然而,只需要 Detroit 剩下 27 场比赛全部获胜,而 New York 剩下 28 场比赛全部失败,Detroit 依然可能成为冠军。有这种可能嘛?要不要说服自己,Detroit 已经在数学上被淘汰呢?
题目把这个问题抽象成了最大流问题。
首先我们需要处理输入数据。由于之后在最大流的计算过程中我们需要以数组下标,即整数,来表示不同的球队,因此需要建立一个 String to Integer 和 Integer to String 的映射。
for (int i = 0; i < numberOfTeams; i++) {
String name = in.readString();
int win = in.readInt();
int lose = in.readInt();
int left = in.readInt();
// 存入 teams,并建立 id 与 name 的互相映射
teams.put(name, new Team(win, lose, left));
teamIndexToTeamName.put(i, name);
teamNameToTeamIndex.put(name, i);
// 在剩余的比赛场次中,与其他各队伍的比赛次数
for (int j = 0; j < numberOfTeams; j++) {
remainingAgainst[i][j] = in.readInt();
}
in.readLine();
}
处理完输入数据,很容易可以实现 wins()、numberOfTeams() 等函数。
为了确定某一支队伍是不是在数学上被淘汰了,我们考虑以下两种情况:
- Trivial elimination. 如果 x 队可以赢得的最大比赛数少于其他 i 队的获胜次数,那么 x 队将被淘汰(如上例中的 Montreal)。也就是说,如果 w[x]+ r[x]< w[i],则从数学上消除了团队 x。
- Nontrivial elimination. 否则,我们将创建一个流动网络并解决其中的最大流问题。
由于 algs4 包中已经实现了 FlowNetwork,所以这次作业的核心其实不在于如何实现一个最大流网络(那个只要抄书、抄网上的代码就可以了),更重要的是如何将一个实际问题抽象为最大流网络的模型。
为了评估队伍 x 是不是在数学上已经被淘汰,就要以除了 x 以外的所有队伍、以及这些队伍之间进行的所有比赛(不包括队伍 x)作为结点,建立加权有向图。
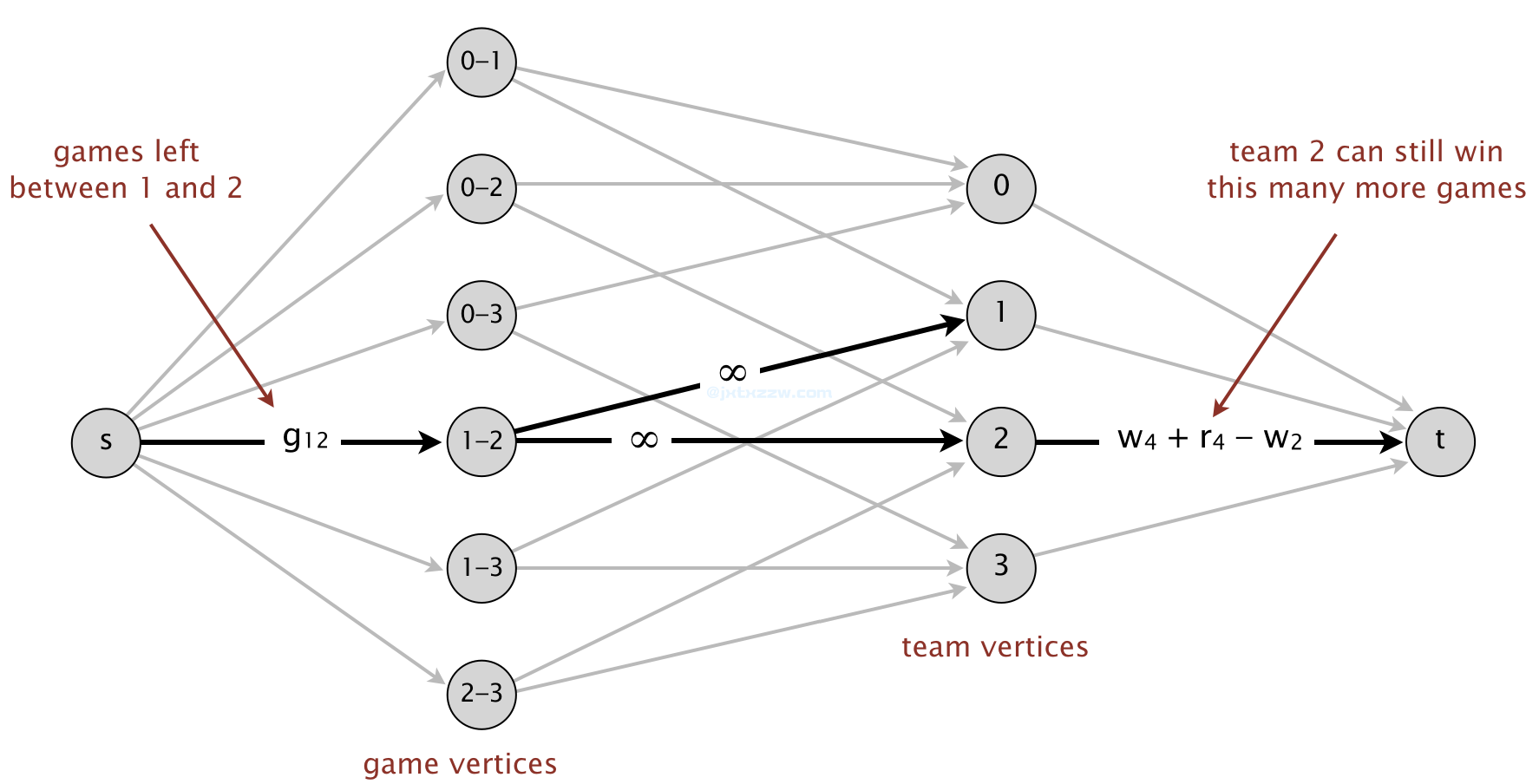
直观地讲,网络中的每一个流量单位都对应着一场剩余的比赛:当它从 s 流向 t 时,它会经过代表一场比赛的顶点,比如说在球队 i 和 j 之间的比赛,然后会通过一个代表球队的顶点,即 i 或 j 中的一个,比如说 i。这意味着,球队 i 和 j 之间的比赛是以球队 i 的胜利作为结果的。
在上图中,从 s 流向 t 的一条网络流先后经过了结点 (1-2) 和 [2],这意味着球队 1 和球队 2 的比赛中获胜方是球队 2。
在构建网络的时候,首先将起点 s 与所有可能发生的比赛(如上图中的 game vertices) (i-j) 连接,并设置容量为球队 i 和球队 j 之间剩余的比赛场次 remainingAgainst[i][j]。如果经过 (i-j) 的流量用尽了整条边上的所有容量,则将其解释为球队 i 和球队 j 之间完成了剩余所有的比赛,并最终分流到结点 i 或者结点 j,即 i 和 j 各自获胜的场数。
// 首先将起点 s 与所有可能发生的比赛(game vertices)连接
for (int i = 0; i < numberOfTeams; i++) {
if (i == x) {
continue;
}
for (int j = i + 1; j < numberOfTeams; j++) {
if (j == x) {
continue;
}
// 起点是 s,game vertices 的编号从 1 开始,限制容量为 remainingAgainst[i][j]
flowNetwork.addEdge(new FlowEdge(s, index, remainingAgainst[i][j]));
}
}
下一步要做的是将 team vertices 与 game vertices 连接,如上图。注意我们只能将对应的球队与确实发生了比赛的场次做连接,但是我们不需要限制这些连接上的容量,即允许任意球队赢得任意场次。尽管事实上获胜的场次不可能大于实际发生比赛的数量,但是由于从起点 s 出发的路径已经限制了容量,这里可以简单将容量设置为无穷大。
// 然后将 team vertices 与 game vertices 连接,容量为无穷大 // 比赛涉及到的双方是 i 和 j,因此代表它们的 team vertices 就是 i(j) + numberOfGameVertices + 1 flowNetwork.addEdge(new FlowEdge(index, i + numberOfGameVertices + 1, Double.POSITIVE_INFINITY)); flowNetwork.addEdge(new FlowEdge(index, j + numberOfGameVertices + 1, Double.POSITIVE_INFINITY));
最后,我们需要将 team vertices 与终点 t 连接。我们想要知道有没有一种可能,使得球队 x 在完成了所有比赛后,能够获得与球队 i 至少相同的获胜场次。由于 x 已经获得了 w[x] 场比赛,而它还剩下 r[x] 场比赛,所以它最多获胜 w[x] + r[x] 场比赛。我们通过限制 team[i] 到终点 t 的容量,来使得球队 i 获胜场数不会超过 w[x] + r[x] – w[i],从而确保 x 获胜的场数是最多的。
// 最后,我们需要将 team vertices 与终点 t 连接,容量限制为 w[x] + r[x] - w[i] int wX = teams.get(team).wins; int rX = teams.get(team).remaining; int wI = teams.get(teamIndexToTeamName.get(i)).wins; flowNetwork.addEdge(new FlowEdge(i + numberOfGameVertices + 1, t, wX + rX - wI));
// 计算当前网络的最大流 FordFulkerson maxFlow = new FordFulkerson(flowNetwork, s, t); // 球队 x 没有被淘汰,当且仅当最大流的值大于等于从 s 出发的所有流量 return flow > maxFlow.value();
如果最大流中所有从 s 指向的边都是满的,那么就相当于按照以下原则分配每一场比赛的获胜方:没有球队会获得比 x 更多的胜利场次。如果有些从 s 指向的边没有满,那么就不存在球队 x 能赢得比赛的情况。
这是因为对于被评估的球队 x 来说,如果有球队 i 在没达到满流量的情况下就获得了与瓶颈(w[x] + r[x] – w[i]),那么球队 i 稍微再努力即可能超越 x 成为冠军,而当球队 i 拼尽全力达到满流量才能和球队 x 获得相同的获胜场次,那么球队 x 将不会被淘汰。
最小切能够说明什么问题?
在给出的例子中,Detroit 最多赢得 49 + 27 = 76 场比赛。而 New York, Baltimore, Boston, Toronto 这四支球队已经获得一共 75 + 71 + 69 + 63 = 278 场胜利。假设它们与 Detroit 的比赛全部失败,即促成 Detroit 获得最高 76 场胜利,那么,它们之间还有 3 + 8 + 7 + 2 + 7 = 27 场比赛,而这 27 场比赛无论结果如何,都会在它们四支球队的累积获胜数上加上 27,因为无论如何,胜利都是它们四支球队中产生,由此,它们一共获胜 305 场比赛,平均每支球队获胜 76.25 场,因此至少有一支球队获胜数大于等于 77 场,即,Detroit 被淘汰。
// subset R of teams that eliminates given team; null if not eliminated
public Iterable<String> certificateOfElimination(String team) {
isValid(team);
if (!isEliminated(team)) {
return null;
}
ArrayList<String> list = new ArrayList<>();
int numberOfGameVertices = numberOfTeams * (numberOfTeams - 1) / 2;
FordFulkerson maxFlow = getMaxFlow(team);
for (int index = 1; index <= numberOfTeams; index++) {
if (maxFlow.inCut(index + numberOfGameVertices)) {
list.add(teamIndexToTeamName.get(index));
}
}
return list;
}
有一个需要注意的地方,容量必须是非负数,所以如果 wX + rX – wI < 0,则意味着可以提前结束判断,认为 x 已经被淘汰。注意如果将 capacity 设置为 Math.max(0, wX + rX – wI) 会导致有些被 eliminate 的球队无法被正确淘汰。
if (wX + rX - wI < 0) {
return null;
} else {
flowNetwork.addEdge(new FlowEdge(i + numberOfGameVertices + 1, t, wX + rX - wI));
}
由此,判断 isEliminated 的时候需要判断是不是 null。
if (maxFlow == null) {
return true;
} else {
// 球队 x 没有被淘汰,当且仅当最大流的值大于等于从 s 出发的所有流量
return flow > maxFlow.value();
}
而在输出子集 R 的时候,如果 maxFlow 是 null,则需要重新计算每一个球队的 wX + rX – wI,将 wX + rX – wI < 0 的全部加入队列。
if (maxFlow == null) {
int wX = teams.get(team).wins;
int rX = teams.get(team).remaining;
int wI = teams.get(teamIndexToTeamName.get(index)).wins;
if (wX + rX - wI < 0) {
list.add(teamIndexToTeamName.get(index));
}
} else if (maxFlow.inCut(index + numberOfGameVertices + 1)) {
list.add(teamIndexToTeamName.get(index));
}
以上代码得分 100 分。
完整代码可以移步:https://gitlab.jxtxzzw.com/jxtxzzw/coursera_assignments 或者 https://www.github.com/jxtxzzw/coursera_assignments
