学校	华东师范大学
专业	计算机科学与技术
课程名称	数字图像处理
教师	童卫青
年份	2018年秋

一、实验目的

1. 了解 OpenCV 是如何使用的。
2. 了解在 C 语言程序中调用 OpenCV 进行图像的读、写、显示。
3. 了解图像的平移变换、放缩变换、旋转、剪切、转化为灰度等操作。
4. 掌握要完成图像的变化，应该用怎么样的矩阵对图像的像素进行操作。

二、实验内容

1. 配置运行环境、导入工程并运行程序，观察结果。
2. 理解代码，理解每一个函数的声明、作用、调用方法。
3. 了解图像的平移变换、放缩变换、旋转、剪切、转化为灰度等操作。

三、实验原理说明

3.1 工程的建立、OpenCV库的导入

老师给的是 Visual Studio 的工程，所以直接导入就可以运行，不需要代码层面的操作。

特别需要说明的是，老师给的是 Visual Studio 2015 的工程，如果本机运行的是 Visual Studio 2017 或者更新版本的程序，绝对不要自己去修改任何的配置信息，直接打开，然后让 Visual Studio 自己完成配置的更新。

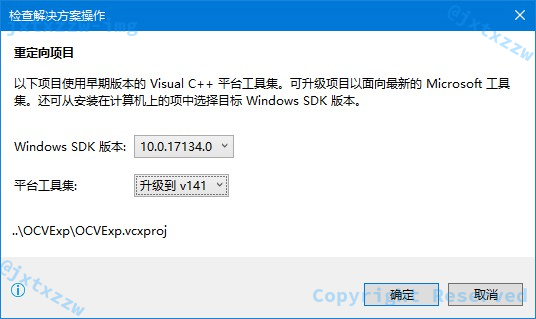
OpenCV 库使用的是项目解决方案的动态链接库，而不是环境变量中的 OpenCV 库，所以理论上就算自己不安装 OpenCV 库也是完全可以使用的，配置信息都在项目文件里写好了。

3.2 一些基本信息的说明

命名空间，也称名字空间、名称空间等，它表示着一个标识符的可见范围。

一个标识符可在多个命名空间中定义，它在不同命名空间中的含义是互不相干的。

这样，在一个新的命名空间中可定义任何标识符，它们不会与任何已有的标识符发生冲突，因为已有的定义都处于其他命名空间中。

由此，代码中使用了using namespace cv，之后就可以直接使用 OpenCV 库的函数，例如imread()等。

#include <stdio.h>
#include "opencv.hpp"
using namespace std;
using namespace cv;

3.3 图像的读入和显示

读入图像使用的是imread()函数，该函数是从文件载入一张图片到内存，具体的函数使用说明参见下文第四部分。

图像的显示首先要创建一个 Windows 窗口程序，然后调用imshow()将一张图片显示在窗口中。

3.4 等待按键

由于程序的运行速度很快，所以从显示一张图片到执行下一段代码非常非常快，可能都来不及看，这显然是不行的，所以这里使用了一个方法——等待按键，来作为“暂停”。

cvWaitKey()是 OpenCV 的一个函数，他会阻塞自己，直到等待到一个按键。

这样，就给用户足够的时间观察变换后的图像，直到用户按下按键或者单击鼠标，才会销毁窗口、继续执行后面的代码。

3.5 图像变换

图像的变换，本质上是一个像素点的坐标经过一系列计算以后得到了一个新的坐标。

图像坐标变换，也称为空间坐标变换或几何坐标变换，是一种位置映射操作，涉及的是图像空间里各个坐标位置间的转换及方式。

图像中的每个像素有一定的空间位置，可借助坐标变换改变其位置，从而使图像改观。

对整幅图像的坐标变换是通过对每个像素进行坐标变换来实现的。

例如，对于某像素点 $(x,y)$ 想要变换到 $(x’,y’)$，就相当于是对矩阵 $\left[\begin{matrix} x \\y \\1\end{matrix}\right]$ 左乘一个矩阵 $\left[\begin{matrix}a & b & c \\d & e & f \\ g & h & i\end{matrix}\right]$，使得这两个矩阵相乘的结果是 $\left[\begin{matrix} x’ \\y’ \\ 1\end{matrix}\right]$。

3.6 图像的存储方式

在我们的 C++ 程序中，OpenCV 的图像打开以后是保存到 Mat 类中的。

Mat 类是一个 $n$ 维密集阵列。

Mat本质上是由两个数据部分组成的类：

• 包含信息有矩阵的大小，用于存储的方法，矩阵存储的地址等的矩阵头
• 包含了像素值的矩阵（可根据选择用于存储的方法采用任何维度存储数据）的一个指针

矩阵头部的大小是恒定的。

然而，矩阵本身的大小因图像的不同而不同，通常是较大的数量级。

特别需要指出的是，如果需要将一张图像赋值给另一个变量，必须使用clone函数。

img1 = imread(fn);

// 拷贝图像
img2 = img1.clone();

如果简单地令

img1 = img2;

那么，img1和img2将指向内存同一块地方，也就是他们表示的是同一个图像。

3.7 变换矩阵的存储方式

变换矩阵是一个矩阵，所以本质上也是一个$n$ 维密集阵列，因此也可以用 Mat 类。

四、函数使用说明

imread

Mat imread(const String& filename, int flags=IMREAD_COLOR )

filename是要加载的文件的名称。

flag是指定加载图像的颜色类型的标志。如果不指定类型，那么默认是IMREAD_COLOR。

可选的flag有：

• CV_LOAD_IMAGE_ANYDEPTH如果置位，当输入具有相应深度时返回 $16$ 位/ $32$ 位图像，否则将其转换为 $8$ 位。
• CV_LOAD_IMAGE_COLOR

  如果设置，则始终将图像转换为彩色图像。

• CV_LOAD_IMAGE_GRAYSCALE

  如果设置，则始终将图像转换为灰度图像。

• 如果值大于 $0$，返回三通道彩色图像。
  • 需要特别说明的是，在当前实现中，会从输出图像中去除 Alpha 通道（如果有的话），如果需要 Alpha 通道，请使用负值。
• 如果值等于 $0$，返回灰度图像。
• 如果值小于 $0$，按原样返回加载的图像（使用Alpha通道）。

函数imread从指定文件加载图像并返回它。如果无法读取图像（由于文件丢失，权限不正确，格式不受支持或无效），该函数返回一个空矩阵（Mat :: data == NULL）。

该函数通过内容而不是文件扩展名确定图像的类型，支持的文件类型有：

• Windows位图 – * .bmp， * .dib
• JPEG文件 – * .jpeg， * .jpg， *。jpe
• JPEG 2000文件 – * .jp2
• 便携式网络图形 – * .png
• WebP – * .webp
• 便携式图像格式 – * .pbm， * .pgm， * .ppm
• 太阳栅格 – * .sr， * .ras
• TIFF文件 – * .tiff， * .tif

由此，我们编写如下代码，就可以载入 lena.jpg 这张图片：

// 读图像文件
cout << "读图像" << endl;

fn = "image\\lena.jpg";
img1 = imread(fn);

// 拷贝图像
img2 = img1.clone();

imwrite

bool imwrite(const String& filename, InputArray img, const vector<int>& params=vector<int>())

filename是文件的名称。

image是要保存的图像。

格式专用的保存编码为对参数 paramId_1， paramValue_1， paramId_2， paramValue_2， ...。

目前支持以下参数：

• 对于JPEG，它可以是从 $0$ 到 $100$ 的质量（CV_IMWRITE_JPEG_QUALITY）（越高越好）。
  • 默认值为 $95$。
• 对于WEBP，它可以是从 $1$ 到 $100$ 的质量（CV_IMWRITE_WEBP_QUALITY）（越高越好）。
  • 默认情况下（不带任何参数），如果质量高于 $100$，则使用无损压缩。
• 对于PNG，它可以是从 $0$ 到 $9$ 的压缩级别（CV_IMWRITE_PNG_COMPRESSION）。
  • 值越大意味着更小的尺寸和更长的压缩时间。默认值为 $3$。
• 对于PPM，PGM或PBM，它可以是二进制格式标志（CV_IMWRITE_PXM_BINARY），$0$ 或 $1$。
  • 默认值为 $1$。

函数imwrite将图像保存到指定的文件。基于文件扩展名选择图像格式。

由此，我们编写如下代码，就可以保存一张图片：

//写图像文件
cout << "写图像" << endl;
fn = "img2.jpg";
imwrite(fn, img2);

namedWindow与moveWindow

void namedWindow(const string＆winname，int flags = WINDOW_AUTOSIZE)

name是窗口标题中可用作窗口标识符的窗口的名称。

flags是窗口支持的标志。

支持的标志是：

• WINDOW_NORMAL如果设置了此项，则用户可以调整窗口大小（无约束）。
• WINDOW_AUTOSIZE

  如果设置了此项，则会自动调整窗口大小以适合显示的图像，并且无法手动更改窗口大小。

• WINDOW_OPENGL

  如果设置了此项，将使用 OpenGL 支持创建窗口。

该函数namedWindow创建一个窗口，可用作图像和轨迹栏的占位符。创建的窗口由其名称引用。

如果已存在具有相同名称的窗口，则该函数不执行任何操作。

void moveWindow(const string＆winname，int x，int y )

winname是窗口名称。

x和y分别是窗口的新的x坐标和y坐标。

由此，我们编写如下代码，就可以新建一个窗口，并将位置调整到左上角：

//创建图像显示窗口
namedWindow("image", CV_WINDOW_AUTOSIZE);
moveWindow("image", 0, 0);

imshow

void imshow(const string＆winname，InputArray mat)

winname是窗口名称。

mat是要显示的图像。

该功能在指定的窗口中显示图像。

如果窗口是使用标志创建的，则图像将以其原始大小显示，但仍然受到屏幕分辨率的限制。

否则，缩放图像以适合窗口。

该功能可能会缩放图像，具体取决于其深度：CV_WINDOW_AUTOSIZE。

• 如果图像是 $8$ 位无符号，则按原样显示。
• 如果图像是 $16$ 位无符号或 $32$ 位整数，则像素除以 $256$，即，值范围 $[0,255 \times 56]$ 被映射到 $[0,255]$。
• 如果图像是 $32$ 位浮点，则像素值乘以 $255$，即，值范围 $[0,1]$ 被映射到 $[0,255]$。

如果在此函数之前未创建窗口，则假定创建一个窗口CV_WINDOW_AUTOSIZE。

如果需要显示大于屏幕分辨率的图像，则需要在显示之前先调用namedWindow("", WINDOW_NORMAL)。

由此，我们编写如下代码，就可以显示一张图片：

//显示图像  
cout << "显示图像" << endl;
imshow("image",img2);
cvWaitKey(0);//等待按键

其中，cvWaitKey是等待按键。

waitKey

int waitKey(int delay = 0) //C++

int cvWaitKey(int delay = 0) //C

delay是以毫秒为单位的延迟。

$0$ 是特殊值，表示“永远”，此时直到按下鼠标按键或者按下键盘按键才会结束。

该函数waitKey无限地（当 $delay \leqslant 0$）等待键事件，或者延迟指定的毫秒数（当 $delay > 0$）。

由于操作系统在切换线程之间的时间有开销，因此该功能不会等待恰好delay毫秒，它将至少等待delay毫秒，具体取决于当时计算机上正在运行的其他内容。

它返回按下的键的代码，如果在指定的时间过去之前没有按下任何键，则返回 $-1$。

cvtColor

void cvtColor(InputArray src, OutputArray dst, int code, int dstCn=0 )

src是输入图像即要进行颜色空间变换的原图像，可以是 Mat 类。

dst是输出图像即进行颜色空间变换后存储图像，也可以是 Mat 类 。

code是转换的代码或标识，即在此确定将什么制式的图片转换成什么制式的图片。

dstCn是目标图像通道数，如果取值为 $0$，则由src和code决定。默认值为 $0$。

转换的代码或标识，有很多，如下：

我们的代码中用到的是CV_RGB2GRAY。

彩色图像转化为灰度图像，最简单的是令R、G、B取三者和的均值，即求出每一个像素在R、G、B三个分量上的均值，再将均值赋值给R、G、B三个分量。

而CV_RGB2GRAY使用的是$\displaystyle I = \alpha \times R + \beta \times G + \gamma \times B$。

这里$\alpha, \beta, \gamma$的取值为$0.299,0.587,0.114$，于是，$\displaystyle I = 0.299 \times R + 0.587 \times G + 0.114 \times B$。

由此，我们编写如下代码，就可以将一张图像转化为灰度图像，并显示：

// 彩色图像转换为灰度图像
cout << "转换为灰度图像" << endl;
Mat grayImage;
cvtColor(img1, grayImage, CV_RGB2GRAY);
imshow("image", grayImage);
cvWaitKey(0);

变换矩阵

Mat 是 OpenCV 的一个类，表示一个矩阵。

该类有很多构造函数，分别可以用不同的参数构造和初始化矩阵。

• Mat (int rows, int cols, int type)
• Mat (Size size, int type)
• Mat (int rows, int cols, int type, const Scalar &s)
• Mat (Size size, int type, const Scalar &s)
• Mat (int ndims, const int *sizes, int type)
• Mat (int ndims, const int *sizes, int type, const Scalar &s)
• Mat (const Mat &m)
• Mat (int rows, int cols, int type, void *data, size_t step=AUTO_STEP)
• Mat (Size size, int type, void *data, size_t step=AUTO_STEP)
• Mat (int ndims, const int *sizes, int type, void *data, const size_t *steps=0)
• Mat (const Mat &m, const Range &rowRange, const Range &colRange=Range::all())
• Mat (const Mat &m, const Rect &roi)
• Mat (const Mat &m, const Range *ranges)

我们的代码中用到的构造函数是

Mat (int rows, int cols, int type)

rows和cols分别表示矩阵的行数和列数。

type表示矩阵的值的类型。

图像的变换本质上可以看做是矩阵的运算。

例如，对于某像素点 $(x,y)$ 想要变换到 $(x’,y’)$，就相当于是对矩阵 $\left[\begin{matrix} x \\y \end{matrix}\right]$ 左乘一个矩阵 $\left[\begin{matrix}a & b & c \\d & e & f \end{matrix}\right]$，使得这两个矩阵相乘的结果是 $\left[\begin{matrix} x’ \\y’ \end{matrix}\right]$。

因为是平面上的图像，所以这个矩阵是 $2$ 行 $3$ 列的。

由此，我们编写如下代码，就可以构造一个变换矩阵：

Mat am(2,3,CV_32FC1);// 2×3变换矩阵

这里的CV_32FC1是定义了一个 $32$ 位的数据类型，是指向一个 $32$ 位数据的地址的指针都可以。

具体地，对该矩阵赋值的方法类似于：

am.at<float>(0, 0) = 1;

at方法接收一个范型的参数，表示数据的数据类型，在上面的代码中，这个数据是float类型的。

之后给定两个值，表示矩阵的行和列，在上面的代码中，指定的是矩阵的第 $0$ 行第 $0$ 列。

于是，上面的代码，在矩阵的第 $0$ 行第 $0$ 列赋值了一个浮点数 $1.0$。

其余各位置也可以通过类似的方法赋值。

由此，我们编写如下代码，就可以对一个变换矩阵赋值，使其变为$\left[\begin{matrix}1 & 0 & 10 \\0 & 1 & 10 \end{matrix}\right]$：

am.at<float>(0, 0) = 1;am.at<float>(0, 1) = 0;am.at<float>(0, 2) = 10;
am.at<float>(1, 0) = 0;am.at<float>(1, 1) = 1;am.at<float>(1, 2) = 10;

warpAffine

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

src是输入图像。

dst是输出具有dsize大小和与src类型相同的图像。

M是一个的变换矩阵。

dsize是输出图像的大小。

flags是插值方法的组合和可选的标记WARP_INVERSE_MAP，表示这M是逆变换（）。

borderMode表示像素外推法，当 borderMode=BORDER_TRANSPARENT，这意味着该功能不会修改与源图像中的异常值对应的目标图像中的像素。

borderValue表示在边界不变的情况下使用的值。默认情况下，它为0。

该函数使用指定的矩阵转换源图像：

由此，我们编写如下代码，就可以对原图像，进行图像变换：

warpAffine(img1, img2, am, img2.size());

这里，我们对img1的每一个像素，左乘变换矩阵am，$\left[\begin{matrix}a & b & c \\d & e & f \end{matrix}\right]$，得到img2的每一个像素。

cvDestroyWindow

void destroyWindow(const string& winname)

winname是需要销毁的窗口的名称。

该函数销毁给定的窗口。

由此，我们编写如下代码，就可以将刚才显示图像的窗口销毁掉，以便结束程序：

cvDestroyWindow("image");

五、实验结果及分析

彩色图像转换为灰度图像

如上文所言，$\displaystyle I = \alpha \times R + \beta \times G + \gamma \times B$。

// 彩色图像转换为灰度图像
cout << "转换为灰度图像" << endl;
Mat grayImage;
cvtColor(img1, grayImage, CV_RGB2GRAY);
imshow("image", grayImage);
cvWaitKey(0);

cvtColor会对img1的每一个像素的R、G、B三个通道进行 $\displaystyle I = 0.299 \times R + 0.587 \times G + 0.114 \times B$ 运算，并将计算后的值作为新的像素点的灰度值。

图像平移变换

平移变换用平移量 $(T_x,T_y)$ 将具有坐标 $(x,y)$ 的点平移到新的位置 $(x’,y’)$。

这可用 $\left[\begin{matrix}1 & 0 & T_x \\0 & 1 & T_y \\ 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}x \\y \\1 \end{matrix}\right]=\left[\begin{matrix}x’ \\y’ \\1 \end{matrix}\right]$ 来表示。

现在想要对图像向右、向下分别平移 $10$ 个单位，那么就是令$T_x=10, T_y = 10$。

于是，变换矩阵为$\left[\begin{matrix}1 & 0 & 10 \\0 & 1 & 10 \end{matrix}\right]$，可通过如下语句赋值：

am.at<float>(0, 0) = 1;am.at<float>(0, 1) = 0;am.at<float>(0, 2) = 10;
am.at<float>(1, 0) = 0;am.at<float>(1, 1) = 1;am.at<float>(1, 2) = 10;

之后用affine变换，并显示：

warpAffine(img1, img2, am,img2.size());
imshow("image", img2);
cvWaitKey(0);

图像缩小变换

图像的放缩矩阵可用 $\left[\begin{matrix}S_x & 0 & 0 \\0 & S_y & 0 \\ 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}x \\y \\1 \end{matrix}\right]=\left[\begin{matrix}x’ \\y’ \\1 \end{matrix}\right]$ 来表示。

现在想要缩小图像到原来的 $\displaystyle \frac{1}{4}$ 倍，那么只需要令 $x$ 像素的每个值变为原来的 $0.5$ 倍且 $y$ 像素的每个值变为原来的 $0.5$ 倍。

于是，变换矩阵为$\left[\begin{matrix}0.5 & 0 & 0 \\0 & 0.5 & 0 \end{matrix}\right]$，可通过如下语句赋值：

am.at<float>(0, 0) = 0.5F; am.at<float>(0, 1) = 0.0F; am.at<float>(0, 2) = 0;
am.at<float>(1, 0) = 0.0F; am.at<float>(1, 1) = 0.5F; am.at<float>(1, 2) = 0;

图像放大变换

与缩小变换类似的，变换矩阵为$\left[\begin{matrix}1.5 & 0 & 0 \\0 & 1.5 & 0 \end{matrix}\right]$，可通过如下语句赋值：

am.at<float>(0, 0) = 1.5F; am.at<float>(0, 1) = 0.0F; am.at<float>(0, 2) = 0;
am.at<float>(1, 0) = 0.0F; am.at<float>(1, 1) = 1.5F; am.at<float>(1, 2) = 0;

图像旋转变换

将一个像素在图像平面上绕旋转轴转 $\gamma$ 角度的旋转变换可用旋转变换矩阵$R_{\gamma}=\left[\begin{matrix}\cos{\gamma} & \sin{\gamma} & 0 \-\sin{\gamma} & \cos{\gamma} & 0 \\ 0 & 0 & 1 \end{matrix}\right]$ 实现。

特别地，如果旋转轴不是坐标原点，那么变换矩阵为$R_{\gamma}=\left[\begin{matrix}\cos{\gamma} & \sin{\gamma} & T_x\cos{\gamma}+T_y\sin{\gamma}-T_x \-\sin{\gamma} & \cos{\gamma} & -T_x\sin{\gamma}+T_y\cos{\gamma}-T_y \\ 0 & 0 & 1 \end{matrix}\right]$ 。

我们的代码中定义旋转角度为 $30$ 度。

float angle = 30;

但是参与运算的是弧度制的，所以想要把角度制的单位转化为弧度制。

float phi = (float)(angle*CV_PI / 180.0F);

上面代码中的CV_PI是 OpenCV 中定义的一个常量，值为 $\pi$。

定义旋转中心为$(256,256)$，得到变换矩阵为$R_{\gamma}=\left[\begin{matrix}\cos{\phi} & -\sin{\phi} & 256 – 256 \times \cos{\phi}+256 \times \sin{\phi} \\ \sin{\phi} & \cos{\phi} & 256 – 256 \times \sin{\phi} – 256 \times \cos{\phi} \\ 0 & 0 & 1 \end{matrix}\right]$

于是，可以用以下代码完成变换矩阵的赋值：

float angle = 30;
int cenx = 256;
int ceny = 256;
float phi = (float)(angle*CV_PI / 180.0F);
am.at<float>(0, 0) = (float)cos(phi); am.at<float>(0, 1) = -(float)sin(phi); am.at<float>(0, 2) = (float)(cenx - cenx * cos(phi) + ceny * sin(phi));
am.at<float>(1, 0) = (float)sin(phi); am.at<float>(1, 1) = (float)cos(phi); am.at<float>(1, 2) = (float)(ceny - cenx * sin(phi) - ceny * cos(phi));

尝试修改旋转中心和旋转角度

例如我尝试修改了旋转中心为 $(100,200)$，旋转角度为 $45$ 度。

即修改代码为 ：

float angle = 45;
int cenx = 100;
int ceny = 200;
float phi = (float)(angle*CV_PI / 180.0F);
am.at<float>(0, 0) = (float)cos(phi); am.at<float>(0, 1) = -(float)sin(phi); am.at<float>(0, 2) = (float)(cenx - cenx * cos(phi) + ceny * sin(phi));
am.at<float>(1, 0) = (float)sin(phi); am.at<float>(1, 1) = (float)cos(phi); am.at<float>(1, 2) = (float)(ceny - cenx * sin(phi) - ceny * cos(phi));

图像剪切变换

剪切令 $x’=x+0.3 \times y$ 且保持 $y$ 不变。

那么矩阵变换就是 $\left[\begin{matrix}1 & 0.3 & 0 \\0 & S_y & 0 \\ 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}x \\y \\1 \end{matrix}\right]=\left[\begin{matrix}x’=x+0.3 \times y \\y’ = y \\1 \end{matrix}\right]$

赋值矩阵就是：

am.at<float>(0, 0) = 1; am.at<float>(0, 1) = 0.3F; am.at<float>(0, 2) = 0;
am.at<float>(1, 0) = 0; am.at<float>(1, 1) = 1.0F; am.at<float>(1, 2) = 0;

进行更多的尝试

am.at<float>(0, 0) = 0.5F; am.at<float>(0, 1) = 0.3F; am.at<float>(0, 2) = 0;
am.at<float>(1, 0) = 0; am.at<float>(1, 1) = 0.8F; am.at<float>(1, 2) = 0;

六、更多尝试与思考

现在网络上很流行的照片美颜、滤镜功能，其实锁起来就是对图像的指定像素进行矩阵变换，也就是对图像的部分区域像素点 $\left[\begin{matrix} x \\y \\ 1\end{matrix}\right]$ 左乘一个矩阵 $\left[\begin{matrix}a & b & c \\d & e & f \\ g & h & i \end{matrix}\right]$。

抛开人工智能的算法，如果只是简单得对图像上的每一个像素左乘一个变换矩阵，那么卷积以后得到的图像，就是对原图像进行滤镜以后的效果。

下面简单尝试一下这件事情。

灰度变换

int gray = (int) (0.299 * c.getRed() + 0.587 * c.getGreen() + 0.114 * c.getBlue());

剪切变换

Blur 滤镜（模糊）

取变换矩阵为$\left[\begin{matrix}\frac{1}{13} & \frac{1}{13} & \frac{1}{13} \\ \frac{1}{13} & \frac{5}{13} &\frac{1}{13} \\ \frac{1}{13}& \frac{1}{13} & \frac{1}{13} \end{matrix}\right]$

Sharpen 滤镜（锐化）

取变换矩阵为$\left[\begin{matrix}0 & -1 & 0 \-1 & 5 &-1 \\ 0 & -1 & 0 \end{matrix}\right]$

Linear 滤镜

取变换矩阵为$\left[\begin{matrix}\frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{1}{9} &\frac{1}{9} \\ \frac{1}{9}& \frac{1}{9} & \frac{1}{9} \end{matrix}\right]$

Edge 滤镜（取边缘）

取变换矩阵为$\left[\begin{matrix}-1 & -1 & -1 \-1 & 8 &-1 \\ -1 & -1 & -1 \end{matrix}\right]$

Emboss 滤镜

取变换矩阵为$\left[\begin{matrix}-1 & 0 & 1 \\ -1 & 1 &1 \\ -1 & 0 & 1 \end{matrix}\right]$

Oil 滤镜

这是一个将图片转化为油画风格的滤镜。

但是严格来说，并不是对每一个像素进行一个矩阵变换。

他的原理是，对于每个像素，遍历他周围的若干个像素，并取周围像素中出现次数最多的那个像素的 RGB 值作为自己的 RGB 值。

我是用 Java 程序简单运行了一下效果。

油画效果还是很明显的。

但是需要注意的是，“周围”必须合理，否则，就会出现下面这个样子：

因为对于每个像素，遍历他周围的若干个像素，这个”周围“太大了，导致大家最后都变成了一样的颜色

不过，也勉强看得出是个猩猩，对吧~~

for (int col = 0; col < pin.width(); col++) {
    for (int row = 0; row < pin.height(); row++) {
        HashMap<Color, Integer> freq = new HashMap<Color, Integer>();
        Color t = null;
        int max = 0;
        for (int i = row - w; i < row + w; i++) {
            for (int j = col - w; j < col + w; j++) {
                if (i >= 0 && i < pin.height() && j >= 0 && j < pin.width()
                    && Math.abs(row - i) + Math.abs(col - j) < w) {
                    Color c = pin.get(j, i);
                    if (freq.containsKey(c)) {
                        freq.put(c, freq.get(c) + 1);
                        if (freq.get(c) > max) {
                            max = freq.get(c);
                            t = new Color(c.getRed(), c.getGreen(), c.getBlue());
                        }
                    } else {
                        freq.put(c, 1);
                        if (freq.get(c) > max) {
                            max = freq.get(c);
                            t = new Color(c.getRed(), c.getGreen(), c.getBlue());
                        }
                    }
                }
            }
        }
        pout.set(col, row, t);
    }
}